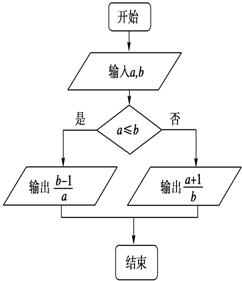
题目内容
7.已知△ABC中,内角A,B,C的对边分别为a,b,c,若$\overrightarrow{m}$=(b+a,-c),$\overrightarrow{n}$=(b-a,a+c),且$\overrightarrow m⊥\overrightarrow n$;(1)求角B的值;
(2)若a=6,b=6$\sqrt{3}$,求△ABC的面积.
分析 (1)由题意可得$\overrightarrow m•\overrightarrow n=(b+a)(b-a)-c(a+c)=0$,由余弦定理可得cosB,结合B的范围即可得解.
(2)由正弦定理可求sinA,结合A的范围可求A,C,由三角形面积公式即可得解.
解答 解:(1)因为$\overrightarrow m⊥\overrightarrow n$,
所以$\overrightarrow m•\overrightarrow n=(b+a)(b-a)-c(a+c)=0$,
即:a2+c2-b2=-ac,
所以$cosB=\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=\frac{-ac}{2ac}=-\frac{1}{2}$,
因为0<B<π,
所以$B=\frac{2π}{3}$.…(4分)
(2)因为$\frac{a}{sinA}=\frac{b}{sinB}$,
所以$sinA=\frac{asinB}{b}=\frac{{6•\frac{{\sqrt{3}}}{2}}}{{6\sqrt{3}}}=\frac{1}{2}$,
因为0<A<π,所以$A=\frac{π}{6}$,$C=π-\frac{2π}{3}-\frac{π}{6}=\frac{π}{6}$,
所以${S_{△ABC}}=\frac{1}{2}absinC=\frac{1}{2}×6×6\sqrt{3}×\frac{1}{2}=9\sqrt{3}$.…(8分)
点评 本题主要考查了正弦定理,余弦定理,三角形面积公式,平面向量及应用,解题时要注意分析角的范围,属于中档题.

练习册系列答案
相关题目
19.双曲线$\frac{x^2}{4}-\frac{y^2}{2}$=1的渐近线方程是( )
| A. | y=±$\sqrt{2}$x | B. | y=±$\frac{{\sqrt{2}}}{2}$x | C. | y=±$\frac{1}{2}$x | D. | y=±2x |