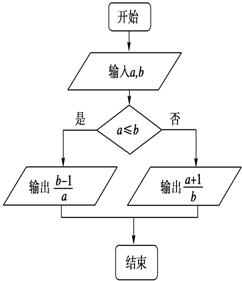
题目内容
10．求函数y=log${\;}_{\frac{1}{2}}$|x+2|的单调增区间（画图象解答）．分析 先去绝对值号，原函数变成$y=\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}（x+2）}&{x＞-2}\\{lo{g}_{\frac{1}{2}}[-（x+2）]}&{x＜-2}\end{array}\right.$，分别分析每段函数和函数$lo{g}_{\frac{1}{2}}x$的关系，从而画出这两段函数，也就画出了原函数，根据函数图象即可写出其单调增区间．
解答 解：$y=lo{g}_{\frac{1}{2}}|x+2|=\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}（x+2）}&{x＞-2}\\{lo{g}_{\frac{1}{2}}-（x+2）}&{x＜-2}\end{array}\right.$；
$lo{g}_{\frac{1}{2}}（x+2）$是$lo{g}_{\frac{1}{2}}x$的图象向左平移2个单位得到；
$lo{g}_{\frac{1}{2}}[-（x+2）]$是先将$lo{g}_{\frac{1}{2}}x$关于y轴对称得到$lo{g}_{\frac{1}{2}}（-x）$，再将该函数图象向左平移2个单位便得到$lo{g}_{\frac{1}{2}}[-（x+2）]$的图象，所以原函数的图象如下所示：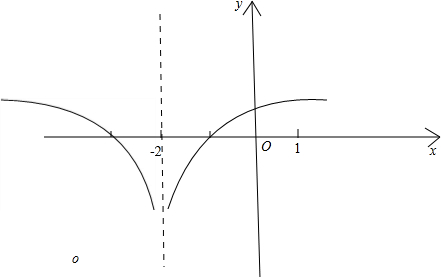
∴由图象可以看出原函数的单调增区间为（-2，+∞）．
点评 考查含绝对值函数的处理方法：去绝对值号，图象的平移变换及对称变换，熟悉对数函数的图象，以及根据函数图象判断函数的单调性．
练习册系列答案
浙江之星课时优化作业系列答案
激活思维优加课堂系列答案
相关题目
5．在极坐标系中，已知两点A（2，$\frac{π}{6}$），B（2，-$\frac{π}{6}$），则|AB|=（ ）
| A． | $\sqrt{3}$ | B． | 2 | C． | 2$\sqrt{3}$ | D． | 4 |
19．双曲线$\frac{x^2}{4}-\frac{y^2}{2}$=1的渐近线方程是（ ）
| A． | y=±$\sqrt{2}$x | B． | y=±$\frac{{\sqrt{2}}}{2}$x | C． | y=±$\frac{1}{2}$x | D． | y=±2x |
20．下列函数f（x）中，满足“对任意x1，x2∈（0，+∞），当x1＜x2时，都有f（x1）＞f（x2）”的是（ ）
| A． | f（x）=$\frac{1}{x}$ | B． | f（x）=x+$\frac{1}{x}$ | C． | f（x）=（x-1）2 | D． | f（x）=ln（x+1） |