题目内容
已知函数f(x)= 的图象过原点,且关于点(-1,2)成中心对称.
的图象过原点,且关于点(-1,2)成中心对称.
(1)求函数f(x)的解析式;
(2)若数列{an}满足a1=2,an+1=f(an),试证明数列 为等比数列,并求出数列{an}的通项公式.
为等比数列,并求出数列{an}的通项公式.
 的图象过原点,且关于点(-1,2)成中心对称.
的图象过原点,且关于点(-1,2)成中心对称.(1)求函数f(x)的解析式;
(2)若数列{an}满足a1=2,an+1=f(an),试证明数列
 为等比数列,并求出数列{an}的通项公式.
为等比数列,并求出数列{an}的通项公式.(1)f(x)=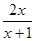 (2)an=
(2)an=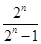
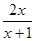 (2)an=
(2)an=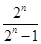
(1)∵f(0)=0,∴c=0.
∵f(x)= 的图象关于点(-1,2)成中心对称,
的图象关于点(-1,2)成中心对称,
∴f(x)+f(-2-x)=4,解得b=2.∴f(x)=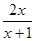 .
.
(2)∵an+1=f(an)=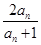 ,
,
∴当n≥2时,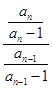 =
=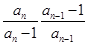 =
=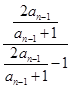 ·
·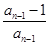 =
=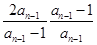 =2.
=2.
又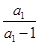 =2≠0,∴数列
=2≠0,∴数列 是首项为2,公比为2的等比数列,∴
是首项为2,公比为2的等比数列,∴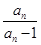 =2n,∴an=
=2n,∴an=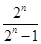 .
.
∵f(x)=
 的图象关于点(-1,2)成中心对称,
的图象关于点(-1,2)成中心对称,∴f(x)+f(-2-x)=4,解得b=2.∴f(x)=
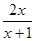 .
.(2)∵an+1=f(an)=
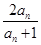 ,
,∴当n≥2时,
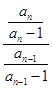 =
=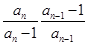 =
=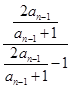 ·
·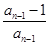 =
=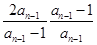 =2.
=2.又
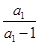 =2≠0,∴数列
=2≠0,∴数列 是首项为2,公比为2的等比数列,∴
是首项为2,公比为2的等比数列,∴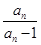 =2n,∴an=
=2n,∴an=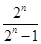 .
.
练习册系列答案
相关题目
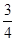 是省外游客,其余是省内游客.在省外游客中有
是省外游客,其余是省内游客.在省外游客中有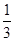 持金卡,在省内游客中有
持金卡,在省内游客中有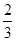 持银卡.(1)在该团中随机采访2名游客,求恰有1人持银卡的概率;
持银卡.(1)在该团中随机采访2名游客,求恰有1人持银卡的概率;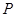 的关系允许近似的满足:
的关系允许近似的满足: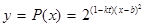 (其中
(其中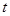 为关税的税率,且
为关税的税率,且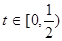 ,
,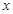 为市场价格,
为市场价格,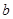 、
、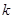 为正常数),当
为正常数),当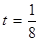 时的市场供应量曲线如图:
时的市场供应量曲线如图: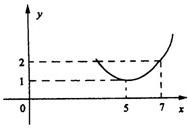
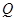 ,它近似满足
,它近似满足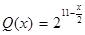 .当
.当 时的市场价格称为市场平衡价格.为使市场平衡价格控制在不低于9元,求税率
时的市场价格称为市场平衡价格.为使市场平衡价格控制在不低于9元,求税率
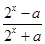 在其定义域上为奇函数”的________条件.(填“充分不必要”“必要不充分”“充要”“既不充分也不必要”)
在其定义域上为奇函数”的________条件.(填“充分不必要”“必要不充分”“充要”“既不充分也不必要”)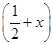 =f
=f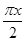 ;④f(x)=ln x+1.其中存在稳定区间的函数有________(写出所有正确命题的序号).
;④f(x)=ln x+1.其中存在稳定区间的函数有________(写出所有正确命题的序号).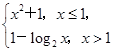 则满足f(x)≤2的x的取值范围是( ).
则满足f(x)≤2的x的取值范围是( ).