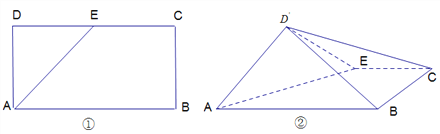
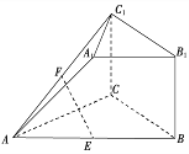
��Ŀ����
����Ŀ����ij�β��Ժ�һλ��ʦ�ӱ���48ͬѧ�������ȡ6λͬѧ�����ǵ����ġ���ʷ�ɼ����±���
ѧ����� | 1 | 2 | 3 | 4 | 5 | 6 |
���ijɼ� | 60 | 70 | 74 | 90 | 94 | 110 |
��ʷ�ɼ� | 58 | 63 | 75 | 79 | 81 | 88 |
(1)���涨���ijɼ�������90��Ϊ���㣬��ʷ�ɼ�������80��Ϊ���㣬��Ƶ�������ʣ��ֱ���Ƹð����ġ���ʷ�ɼ������������
(2)���ϱ����ݻ���ɢ��ͼ������ʷ�ɼ�![]() �����ijɼ�
�����ijɼ�![]() ���н�ǿ��������ع�ϵ����
���н�ǿ��������ع�ϵ����![]() ��
��![]() �����Իع鷽�̣�ϵ����ȷ��0.1��.
�����Իع鷽�̣�ϵ����ȷ��0.1��.
�ο���ʽ���ع�ֱ�߷�����![]() ������
������![]() ��
�� ![]()
���𰸡���1�����ġ���ʷ�ɼ�����������ֱ�Ϊ24��16����2��![]() .
.
�������������������1���ɱ������ݵó����ġ���ʷ�ɼ�Ϊ�����Ƶ�ʣ��Ӷ�����ð����ġ���ʷ�ɼ��������������2���ɱ������ݼ���![]() ������ع�ϵ����д�����Իع鷽��.
������ع�ϵ����д�����Իع鷽��.
���������1���ɱ������ݣ����ijɼ�����ʷ�ɼ�Ϊ�����Ƶ�ʷֱ�Ϊ![]()
�ʸð����ġ���ʷ�ɼ�����������ֱ�Ϊ24��16
��2���ɱ������ݿɵã� ![]()
![]() ��
�� ![]()
���ԣ� 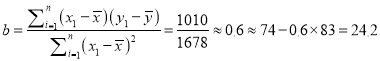
����![]() ��
��![]() �����Իع鷽��Ϊ
�����Իع鷽��Ϊ![]() .
.

 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д�����Ŀ��ij�㷨�ij���ͼ��ͼ��ʾ����������ı���x��1��2��3������30��30�������еȿ������������ 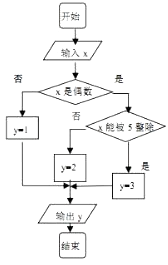
��1���ֱ�����������ͼ��ȷ�������ʱ���y��ֵΪi�ĸ���Pi��i=1��2��3����
��2���ס�����ͬѧ�����Լ��Գ����ͼ�����⣬���Ա�д�����ظ�����n�κ�ͳ�Ƽ�¼�����y��ֵΪi��i=1��2��3����Ƶ���������Ǽס�������Ƶ��ͳ�Ʊ��IJ������ݣ� ��Ƶ��ͳ�Ʊ������֣�
���д��� | ���y=1��Ƶ�� | ���y=2��Ƶ�� | ���y=3��Ƶ�� |
50 | 24 | 19 | 7 |
�� | �� | �� | �� |
2000 | 1027 | 776 | 197 |
�ҵ�Ƶ��ͳ�Ʊ������֣�
���д��� | ���y=1��Ƶ�� | ���y=2��Ƶ�� | ���y=3��Ƶ�� |
50 | 26 | 11 | 13 |
�� | �� | �� | �� |
2000 | 1051 | 396 | 553 |
��n=2000ʱ�����ݱ��е����ݣ��ֱ�д���ס����������������y��ֵΪi��i=1��2��3����Ƶ�ʣ��÷�����ʾ�������жϼס�����˭����д�ij�������㷨Ҫ��Ŀ����Խϴ�
����Ŀ����ijУ��һ�꼶ѧ���μ����������������ͳ�ƣ������ȡ![]() ��ѧ����Ϊ�������õ���
��ѧ����Ϊ�������õ���![]() ��ѧ���μ���������Ĵ���.���ݴ�����������Ƶ����Ƶ�ʵ�ͳ�Ʊ���Ƶ�ʷֲ�ֱ��ͼ���£�
��ѧ���μ���������Ĵ���.���ݴ�����������Ƶ����Ƶ�ʵ�ͳ�Ʊ���Ƶ�ʷֲ�ֱ��ͼ���£�
���� | Ƶ�� | Ƶ�� |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
�ϼ� |
| 1 |

��1���������![]() ��ͼ��
��ͼ��![]() ��ֵ��
��ֵ��
��2���Թ������Dzμ����������ƽ��������
��3������ȡ�����У��Ӳμ���������Ĵ���������20�ε�ѧ������ѡ2�ˣ�������1�˲μ������������������![]() �ڵĸ���.
�ڵĸ���.