题目内容
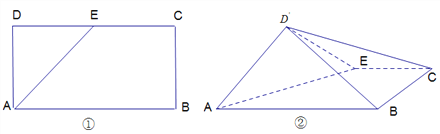
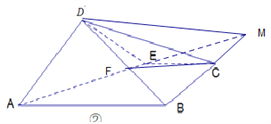
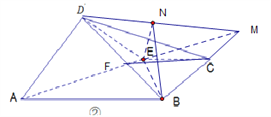
【题目】如图①,在矩形![]() 中,
中, ![]() ,
, ![]() 是
是![]() 的中点,将三角形
的中点,将三角形![]() 沿
沿![]() 翻折到图②的位置,使得平面
翻折到图②的位置,使得平面![]() 平面
平面![]() .
.
(Ⅰ)在线段![]() 上确定点
上确定点![]() ,使得
,使得![]() 平面
平面![]() ,并证明;
,并证明;
(Ⅱ)求![]() 与
与![]() 所在平面构成的锐二面角的正切值.
所在平面构成的锐二面角的正切值.
【答案】(1)点![]() 是线段
是线段![]() 中点时,
中点时, ![]() 平面
平面![]() ,证明见解析;(2)
,证明见解析;(2)![]() .
.
【解析】试题分析:(Ⅰ) ![]() ,
, ![]() 的延长线交于点
的延长线交于点![]() ,由已知可得点
,由已知可得点![]() 是
是![]() 的中点,取BD的中点
的中点,取BD的中点![]() ,由三角形的中位线可得
,由三角形的中位线可得![]() ,可证;(2)由条件可得
,可证;(2)由条件可得![]() ,进而可得
,进而可得![]()
![]() 平面
平面![]() .在平面
.在平面![]() 内作
内作![]()
![]()
![]() ,由线面垂直的性质可得
,由线面垂直的性质可得![]()
![]()
![]() .所以
.所以![]() 就是
就是![]() 与
与![]() 所在平面构成的锐二面角的平面角.求角即可。
所在平面构成的锐二面角的平面角.求角即可。
试题解析:(Ⅰ)点![]() 是线段
是线段![]() 中点时,
中点时, ![]() 平面
平面![]() .
.
证明:记![]() ,
, ![]() 的延长线交于点
的延长线交于点![]() ,因为
,因为![]() ,所以点
,所以点![]() 是
是![]() 的中点,
的中点,
所以![]() .
.
而![]() 在平面
在平面![]() 内,
内, ![]() 在平面
在平面![]() 外,
外,
所以![]() 平面
平面![]() .
.
(Ⅱ)在矩形![]() 中,
中, ![]() ,
, ![]() ,
,
因为平面![]()
![]() 平面
平面![]() ,且交线是
,且交线是![]() ,
,
所以![]()
![]() 平面
平面![]() .
.
在平面![]() 内作
内作![]()
![]()
![]() ,连接
,连接![]() ,
,
则![]()
![]()
![]() .
.
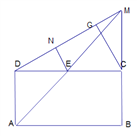
所以![]() 就是
就是![]() 与
与![]() 所在平面构成的锐
所在平面构成的锐
二面角的平面角.
因为![]() ,
, ![]() ,
,
所以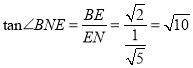 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】在某次测试后,一位老师从本班48同学中随机抽取6位同学,他们的语文、历史成绩如下表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 |
语文成绩 | 60 | 70 | 74 | 90 | 94 | 110 |
历史成绩 | 58 | 63 | 75 | 79 | 81 | 88 |
(1)若规定语文成绩不低于90分为优秀,历史成绩不低于80分为优秀,以频率作概率,分别估计该班语文、历史成绩优秀的人数;
(2)用上表数据画出散点图易发现历史成绩![]() 与语文成绩
与语文成绩![]() 具有较强的线性相关关系,求
具有较强的线性相关关系,求![]() 与
与![]() 的线性回归方程(系数精确到0.1).
的线性回归方程(系数精确到0.1).
参考公式:回归直线方程是![]() ,其中
,其中![]() ,
, ![]()