题目内容
【题目】某算法的程序图如图所示,其中输入的变量x在1,2,3,…,30这30个整数中等可能随机产生. 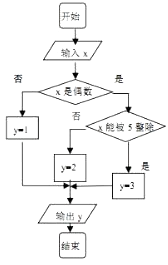
(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数,下面是甲、乙所作频数统计表的部分数据: 甲的频数统计表(部分)
运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
50 | 24 | 19 | 7 |
… | … | … | … |
2000 | 1027 | 776 | 197 |
乙的频数统计表(部分)
运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
50 | 26 | 11 | 13 |
… | … | … | … |
2000 | 1051 | 396 | 553 |
当n=2000时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断甲、乙中谁所编写的程序符合算法要求的可能性较大.
【答案】
(1)解:由题意可得,变量x是从1,2,3,…30这30个整数中可能随机产生的一个数,共有30中结果,
当变量x从1,3,5,7,9,11,13,15,17,19,21,23,25,27,29这15个整数中产生时,输出y的值为1,所以P1= ![]() ,
,
当变量x从2,4,6,8,12,14,16,18,22,24,26,28这12个整数中产生时,输出原点值为2,所以P2= ![]() ,
,
当变量x从10,20,30这3个整数中产生时,输出y的值为3,所以P3= ![]()
(2)解:当n=2000时,甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率如下,
n=2000 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
甲 |
|
|
|
乙 |
|
|
|
比较频率可得,乙所编程序符合算法要求的可能性较大
【解析】(1)变量x是在1,2,3,…,24这24个整数中随机产生的一个数,共有24种可能,由程序框图可得y值为1,2,3对应的情况,由古典概型可得;(2)由题意可得当n=2100时,甲、乙所编程序各自输出的y值为1,2,3时的频率,可得答案

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案【题目】在某次测试后,一位老师从本班48同学中随机抽取6位同学,他们的语文、历史成绩如下表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 |
语文成绩 | 60 | 70 | 74 | 90 | 94 | 110 |
历史成绩 | 58 | 63 | 75 | 79 | 81 | 88 |
(1)若规定语文成绩不低于90分为优秀,历史成绩不低于80分为优秀,以频率作概率,分别估计该班语文、历史成绩优秀的人数;
(2)用上表数据画出散点图易发现历史成绩![]() 与语文成绩
与语文成绩![]() 具有较强的线性相关关系,求
具有较强的线性相关关系,求![]() 与
与![]() 的线性回归方程(系数精确到0.1).
的线性回归方程(系数精确到0.1).
参考公式:回归直线方程是![]() ,其中
,其中![]() ,
, ![]()