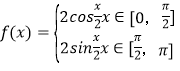题目内容
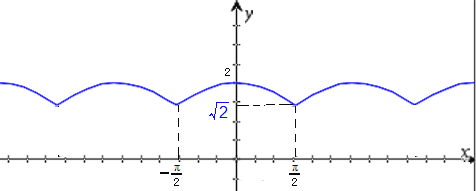
【题目】函数的性质通常指函数的定义域、值域、周期性、单调性、奇偶性、对称性等,请选择适当的探究顺序,研究函数![]() 的性质,并在此基础上填写下表,作出f(x)在区间[-π,2π]上的图象.
的性质,并在此基础上填写下表,作出f(x)在区间[-π,2π]上的图象.
性质 | 理由 | 结论 | 得分 |
定义域 | |||
值域 | |||
奇偶性 | |||
周期性 | |||
单调性 | |||
对称性 | |||
作图 |
| ||
【答案】详见解析
【解析】
由正弦函数的最大最小值,可得函数的定义域为R;由平方法结合余弦函数的有界性,得到函数的值域为[![]() ,2];由函数周期性的定义加以验证,得到函数的最小正周期为π;讨论函数在区间[0,π]上的单调性,结合函数的周期可得函数在R上的单调区间;最后根据函数奇偶性的定义和轴对称的有关公式,算出f(x)在其定义域上为偶函数,图象关于直线
,2];由函数周期性的定义加以验证,得到函数的最小正周期为π;讨论函数在区间[0,π]上的单调性,结合函数的周期可得函数在R上的单调区间;最后根据函数奇偶性的定义和轴对称的有关公式,算出f(x)在其定义域上为偶函数,图象关于直线![]() 对称.由此即可得到本题的答案.
对称.由此即可得到本题的答案.
∵1-sinx≥0且1+sinx≥0,在R上恒成立
∴函数的定义域为R;
∵![]() =2+2|cosx|
=2+2|cosx|
∴由|cosx|∈[0,1],f2(x)∈[2,4],可得函数的值域为[![]() ,2];
,2];
∵![]() =f(x)
=f(x)
∴函数的最小正周期为π
∵当x∈[0,![]() ]时,
]时,![]() =2cos
=2cos![]() ,在[0,
,在[0,![]() ]上为减函数
]上为减函数
当x∈[![]() ,π]时,
,π]时,![]() =2sin
=2sin![]() ,在[
,在[![]() ,π]上为增函数
,π]上为增函数
∴f(x)在![]() 上递增,在
上递增,在![]() 上递减(k∈Z)
上递减(k∈Z)
∵f(-x)=f(x)且![]() ,
,
∴f(x)在其定义域上为偶函数,结合周期为π得到图象关于直线![]() 对称
对称
因此,可得如下表格:
性质 | 理由 | 结论 | 得分 |
定义域 | -1≤sinx≤1 | 定义域R | |
值域 | y2=2+2|cosx|∈[2,4] | 值域 | |
奇偶性 | f(-x)=f(x) | 偶函数 | |
周期性 | f(x+π)=f(x) | 周期T=π | |
单调性 |
| 在 在 | |
对称性 | f(-x)=f(x), | 关于直线 | |
作图 |
| ||

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目