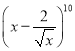题目内容
【题目】已知函数f(x),g(x)满足关系g(x)=f(x)f(x+α),其中α是常数.
(1)设f(x)=cosx+sinx,![]() ,求g(x)的解析式;
,求g(x)的解析式;
(2)设计一个函数f(x)及一个α的值,使得![]() ;
;
(3)当f(x)=|sinx|+cosx,![]() 时,存在x1,x2∈R,对任意x∈R,g(x1)≤g(x)≤g(x2)恒成立,求|x1-x2|的最小值.
时,存在x1,x2∈R,对任意x∈R,g(x1)≤g(x)≤g(x2)恒成立,求|x1-x2|的最小值.
【答案】(1)![]() (2)f(x)=2cosx,α=-
(2)f(x)=2cosx,α=-![]() (3)
(3)![]()
【解析】
(1)求出f(x+α),代入g(x)=f(x)f(x+α)化简得出.
(2)对g(x)化简得![]() =4cosxcos(x-
=4cosxcos(x-![]() ),故f(x)=2cosx,α=-
),故f(x)=2cosx,α=-![]() .
.
(3)求出g(x)的解析式,由题意得g(x1)为最小值,g(x2)为最大值,求出x1,x2,从而得到|x1-x2|的最小值.
(1)∵f(x)=cosx+sinx,![]() ∴f(x+α)=cos(x+
∴f(x+α)=cos(x+![]() )+sin(x+
)+sin(x+![]() )=cosx-sinx;
)=cosx-sinx;
∴g(x)=(cosx+sinx)(cosx-sinx)=cos2x-sin2x=cos2x.
(2)∵![]() =4cosxcos(x-
=4cosxcos(x-![]() ),
),
∴f(x)=2cosx,α=-![]() .
.
(3)∵f(x)=|sinx|+cosx,∴g(x)=f(x)f(x+α)=(|sinx|+cosx)(|cosx|-sinx)
= ,
,
因为存在x1,x2∈R,对任意x∈R,g(x1)≤g(x)≤g(x2)恒成立,
所以当x1=2kπ+π或![]() 时,g(x)≥g(x1)=-1
时,g(x)≥g(x1)=-1
当![]() 时,g(x)≤g(x2)=2
时,g(x)≤g(x2)=2
所以![]()
或![]()
所以|![]() .
.

 黄冈冠军课课练系列答案
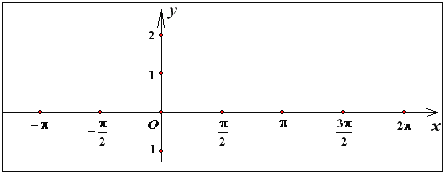
黄冈冠军课课练系列答案【题目】函数的性质通常指函数的定义域、值域、周期性、单调性、奇偶性、对称性等,请选择适当的探究顺序,研究函数![]() 的性质,并在此基础上填写下表,作出f(x)在区间[-π,2π]上的图象.
的性质,并在此基础上填写下表,作出f(x)在区间[-π,2π]上的图象.
性质 | 理由 | 结论 | 得分 |
定义域 | |||
值域 | |||
奇偶性 | |||
周期性 | |||
单调性 | |||
对称性 | |||
作图 |
| ||