题目内容
【题目】在数列![]() 中,
中, ![]() 且
且![]() .
.
(1)求出![]() ,
,![]() ,
,![]() ;
;
(2)归纳猜想出数列![]() 的通项公式;
的通项公式;
(3)证明通项公式![]() .
.
【答案】(1)![]() ,
, ![]() ,
, ![]() (2)
(2)![]() (3)见解析
(3)见解析
【解析】试题分析:(1)依次代入n=1,2,3得![]() ,
, ![]() ,
, ![]() (2)根据分子规律得
(2)根据分子规律得![]() 1,由分母规律得
1,由分母规律得![]() ,即得数列
,即得数列![]() 的通项公式;(3)利用数学归纳法进行证明,由
的通项公式;(3)利用数学归纳法进行证明,由![]() 证明 n=k+1时成立.
证明 n=k+1时成立.
试题解析: (1)![]() ,
, ![]() ,
, ![]() (2)
(2)![]() (3)数学归纳法证明如下:
(3)数学归纳法证明如下:
(1)n=1时成立;(2)假设n=k成立,则![]() ,所以n=k+1时,
,所以n=k+1时, ![]() ,由(1)(2)得结论成立
,由(1)(2)得结论成立
点睛: 用数学归纳法证明等式的策略(1)用数学归纳法证明等式问题是常见题型,其关键点在于弄清等式两边的构成规律,等式两边各有多少项,以及初始值n0的值.(2)由n=k到n=k+1时,除考虑等式两边变化的项外还要充分利用n=k时的式子,即充分利用假设,正确写出归纳证明的步骤,从而使问题得以证明.

练习册系列答案
相关题目
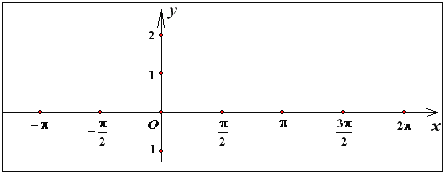
【题目】函数的性质通常指函数的定义域、值域、周期性、单调性、奇偶性、对称性等,请选择适当的探究顺序,研究函数![]() 的性质,并在此基础上填写下表,作出f(x)在区间[-π,2π]上的图象.
的性质,并在此基础上填写下表,作出f(x)在区间[-π,2π]上的图象.
性质 | 理由 | 结论 | 得分 |
定义域 | |||
值域 | |||
奇偶性 | |||
周期性 | |||
单调性 | |||
对称性 | |||
作图 |
| ||
【题目】假设某种设备使用的年限x(年)与所支出的维修费用y(万元)有以下统计资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2 | 4 | 5 | 6 | 7 |
若由资料知y对x呈线性相关关系。试求:
(1)求![]() ; (2)线性回归方程
; (2)线性回归方程![]() ;
;
(3)估计使用10年时,维修费用是多少?
附:利用“最小二乘法”计算a,b的值时,可根据以下公式: