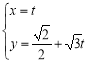题目内容
【题目】已知圆![]() 满足:①圆心在第一象限,截
满足:①圆心在第一象限,截![]() 轴所得弦长为2;②被
轴所得弦长为2;②被![]() 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为![]() ;③圆心到直线
;③圆心到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)若点![]() 是直线
是直线![]() 上的动点,过点
上的动点,过点![]() 分别做圆
分别做圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
, ![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
【答案】(Ⅰ)![]() (Ⅱ)证明见解析
(Ⅱ)证明见解析
【解析】试题分析:(Ⅰ)设出圆![]() 的圆心坐标,可得到圆
的圆心坐标,可得到圆![]() 截
截![]() 轴所得劣弧对的圆心角为
轴所得劣弧对的圆心角为![]() ,由垂径定理得到圆截
,由垂径定理得到圆截![]() 轴的弦长,找出
轴的弦长,找出![]() 及
及![]() 的关系式,,联立得到
的关系式,,联立得到![]() 的关系式;然后利用点到直线的距离公式求出
的关系式;然后利用点到直线的距离公式求出![]() 到直线
到直线![]() 的距离,让其等于
的距离,让其等于![]() ,从而得到
,从而得到![]() 的又一关系式,可求出
的又一关系式,可求出![]() 的值,得到圆心
的值,得到圆心![]() 的坐标,然后利用
的坐标,然后利用![]() 求出圆的半径
求出圆的半径![]() r,根据圆心和半径写出圆的方程即可.
r,根据圆心和半径写出圆的方程即可.
(Ⅱ)设点![]() 以
以![]() 为圆心,
为圆心, ![]() 为半径的圆的方程为
为半径的圆的方程为![]() 又(
又(![]() 由①②得
由①②得![]() ,即(
,即(![]() 可得直线PQ过定点
可得直线PQ过定点![]()
试题解析:(Ⅰ)设圆![]() 的圆心为
的圆心为![]() (
(![]() ,
, ![]() ),半径为
),半径为![]() ,
,
则点![]() 到
到![]() 轴,
轴, ![]() 轴的距离分别为
轴的距离分别为![]() ,
, ![]() .
.
由题设知圆![]() 截
截![]() 轴所得劣弧对的圆心角为
轴所得劣弧对的圆心角为![]() ,知圆
,知圆![]() 截
截![]() 轴所得的弦长为
轴所得的弦长为![]() ,
,
故![]() ,
,
又圆![]() 被
被![]() 轴所截得的弦长为2,所以有
轴所截得的弦长为2,所以有![]() ,从而得
,从而得![]() .
.
又因为![]() 到直线
到直线![]() 的距离为
的距离为![]() ,所以
,所以![]() ,
,
即有![]() ,由此有
,由此有![]() 或
或![]() .
.
解方程组得![]() 或
或![]() (舍)
(舍)
于是![]() ,所求圆的方程是
,所求圆的方程是![]()
(Ⅱ)设点![]() 的坐标为
的坐标为![]() ,
, ![]()
以点![]() 为圆心,以
为圆心,以![]() 为半径圆
为半径圆![]() 的方程为
的方程为![]() ,
,
联立圆![]() 和圆
和圆![]() 的方程:
的方程: 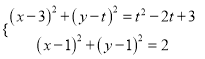
得直线![]() 的方程为:
的方程为: ![]()
即![]() ,直线
,直线![]() 过定点
过定点![]() .
.

练习册系列答案
相关题目