题目内容
【题目】设![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)求![]() 在[-5,
在[-5, ![]() ]的最大值与最小值.
]的最大值与最小值.
【答案】(1)单调增区间为(-2, ![]() ),单调减区间为(-∞,-2)和(
),单调减区间为(-∞,-2)和(![]() ,+∞);(2)f (x)取最小值是0,f (x)取最大值是63.
,+∞);(2)f (x)取最小值是0,f (x)取最大值是63.
【解析】试题分析:
(1)求导可得f ′(x)= -(x+2)(3x-2),利用导函数研究函数的单调性可得单调增区间为(-2, ![]() ),单调减区间为(-∞,-2)和(
),单调减区间为(-∞,-2)和(![]() ,+∞);
,+∞);
(2)由题意结合(1)的结论考查极值和端点处的函数值可得x= -2时,f (x)取最小值0,x= -5时,f (x)取最大值63.
试题解析:
(1)f ′(x)= -(x+2)(3x-2),
令f ′(x)>0得 -2<x<![]() ,令f ′(x)<0得x<-2或x>
,令f ′(x)<0得x<-2或x>![]() ,
,
∴单调增区间为(-2, ![]() ),单调减区间为(-∞,-2)和(
),单调减区间为(-∞,-2)和(![]() ,+∞);
,+∞);
(2)由单调性可知,当x= -2时,f (x)有极小值f (-2 )=0,当x=![]() 时,f (x)有极大值f (
时,f (x)有极大值f (![]() )=
)=![]() ;
;
又f (-5)=63,f (![]() )=
)=![]() ,∴x= -2时,f (x)取最小值0,x= -5时,f (x)取最大值63.
,∴x= -2时,f (x)取最小值0,x= -5时,f (x)取最大值63.

练习册系列答案
相关题目
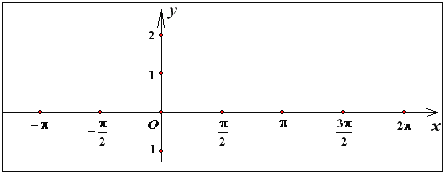
【题目】函数的性质通常指函数的定义域、值域、周期性、单调性、奇偶性、对称性等,请选择适当的探究顺序,研究函数![]() 的性质,并在此基础上填写下表,作出f(x)在区间[-π,2π]上的图象.
的性质,并在此基础上填写下表,作出f(x)在区间[-π,2π]上的图象.
性质 | 理由 | 结论 | 得分 |
定义域 | |||
值域 | |||
奇偶性 | |||
周期性 | |||
单调性 | |||
对称性 | |||
作图 |
| ||