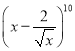题目内容
【题目】若函数
与
的图像有两个不同交点，则实数
的取值范围是（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】函数
过
点，函数
，也过
点，即函数
与
的图至少有一个交点
， 
，函数
在
点处
的切线方程为
， 由
，得
时， 
，此时
是
的切线，即
时，函数
与函数
都在
处与直线
相切，因为
的图象下凹， 
的图象上凸，所以
与
的图象只有一个交点
，当
时，抛物线开口变小，在区间
上
与
的图象有一个交点，共有两个公共点，当
时，抛物线开口变大，在
上有一个交点，共有两个，综上函数
与
的图象有两个不同交点，则实数
的取值范围是
，故选C.
【方法点晴】本题主要考查利用导数求曲线切线方程以及利用导数研究函数的图象与性质，属于难题.求曲线切线方程的一般步骤是：（1）求出
在
处的导数，即
在点
出的切线斜率（当曲线
在
处的切线与
轴平行时，在 处导数不存在，切线方程为
）；（2）由点斜式求得切线方程
.
练习册系列答案
相关题目
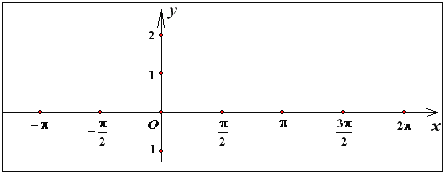
【题目】函数的性质通常指函数的定义域、值域、周期性、单调性、奇偶性、对称性等，请选择适当的探究顺序，研究函数
的性质，并在此基础上填写下表，作出f（x）在区间[-π，2π]上的图象．
性质 | 理由 | 结论 | 得分 |
定义域 | |||
值域 | |||
奇偶性 | |||
周期性 | |||
单调性 | |||
对称性 | |||
作图 |
| ||
【题目】假设某种设备使用的年限x（年）与所支出的维修费用y（万元）有以下统计资料：
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2 | 4 | 5 | 6 | 7 |
若由资料知y对x呈线性相关关系。试求：
（1）求
； （2）线性回归方程
；
（3）估计使用10年时，维修费用是多少？
附：利用“最小二乘法”计算a,b的值时,可根据以下公式：
