题目内容
10.已知集合$A=\left\{{\left.x\right|{2^{{x^2}-x-2}}≤1}\right\}$,B={x|y=ln(1-x)},则A∩∁RB=( )| A. | (1,2) | B. | [1,2] | C. | [-1,1) | D. | (-1,1) |
分析 先根据指数函数和对数函数的性质求出集合A,B,再根据补集的定义求出∁RB,最后根据交集的定义求出答案.
解答 解:由已知得A={x|x2-x-2≤0}={x|-1≤x≤2},
由1-x>0,得x<1,所以B={x|x<1},CRB={x|x≥1|},
∴A∩CRB={x|1≤x≤2},
故选:B.
点评 本题考查指数不等式,函数定义域、集合运算等基础知识,意在考查基本运算能力.

练习册系列答案
相关题目
3.下列不等式(组)的解为{x|x<0}的是( )
| A. | $\frac{x}{2}$-3<$\frac{x}{3}$-3 | B. | $\left\{\begin{array}{l}{x-2<0}\\{2-3x>1}\end{array}\right.$ | C. | x2-2x>0 | D. | |x-1|<2 |
18.“m=3”是“函数f(x)=xm为实数集R上的奇函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
20.在△ABC中,E、F分别为AB、AC上的点,且AE:EB=AF:FC=1:2,P为EF上任一点,实数x、y满足$\overrightarrow{PA}$+x$\overrightarrow{PB}$+y$\overrightarrow{PC}$=$\overrightarrow{0}$,设△ABC、△PBC、△PCA、△PAB的面积分别为S、S1、S2、S3,记$\frac{{S}_{1}}{S}$=λ1,$\frac{{S}_{2}}{S}$=λ2,$\frac{{S}_{3}}{S}$=λ3,则当λ2•λ3取最大值时,2x+y的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | 1 | D. | $\frac{3}{2}$ |
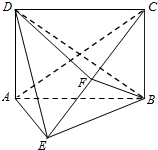 如图,在四棱锥E-ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,
如图,在四棱锥E-ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,