题目内容
5.设函数f(x)=lnx,$\begin{array}{l}{\;}{g(x)=({2-a})({x-1})-2f(x)}\end{array}$.(Ⅰ)当a=1时,求函数g(x)的单调区间;
(Ⅱ)若对任意$x∈({0,\frac{1}{2}}),g(x)>0$恒成立,求实数a的最小值.
分析 (1)先求导,根据导数和函数单调性的关系即可得出;
(2)对于恒成立的问题,分离参数,构造函数,求出函数的最值即可.
解答 解:(1)g(x)的定义域为(0,+∞),
当a=1时,g(x)=x-1-2lnx,
∴g′(x)=1-$\frac{2}{x}$=$\frac{x-2}{x}$,
当x∈(0,2)时,g′(x)<0,g(x)单调递减,
当x∈(2,+∞)时,g'(x)>0,g(x)单调递增,
综上,g(x)的单调递增区间为(2,+∞),单调递减区间为(0,2),
(2)由题意知:(2-a)(x-1)-2lnx>0,在$x∈({0,\frac{1}{2}})$上恒成立,
即(a-2)(1-x)>2lnx在区间$({0,\frac{1}{2}})$上恒成立,
又1-x>0,
∴$a>2+\frac{2lnx}{1-x}$在区间$({0,\frac{1}{2}})$上恒成立,
设$h(x)=2+\frac{2lnx}{1-x}$,$x∈({0,\frac{1}{2}})$,
则$h'(x)=\frac{{\frac{2}{x}({1-x})+2lnx}}{{{{({1-x})}^2}}}=\frac{{\frac{2}{x}-2+2lnx}}{{{{({1-x})}^2}}}$
又令$m(x)=\frac{2}{x}-2+2lnx,x∈({0,\frac{1}{2}})$,
则$m'(x)=-\frac{2}{x^2}+\frac{2}{x}=\frac{-2+2x}{x^2}$
当$x∈({0,\frac{1}{2}})$时,m'(x)<0,m(x)单调递减,
∴$m(x)>m({\frac{1}{2}})=4-2-2ln2>0$,
即h'(x)>0在$({0,\frac{1}{2}})$恒成立,
所以h(x)在$({0,\frac{1}{2}})$单调递增,
∴$h(x)<h({\frac{1}{2}})=2+\frac{{2ln\frac{1}{2}}}{{\frac{1}{2}}}=2-4ln2$,
故a≥2-4ln2,
所以实数a的最小值为2-4ln2.
点评 本题主要考查了函数导数与单调性,主要是利用导数研究函数的单调性等基础知识,考查计算能力和分析问题的能力,以及分类讨论思想,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案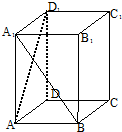 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
| A. | $2\sqrt{2}$ | B. | $\frac{{3\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
| A. | (1,2) | B. | [1,2] | C. | [-1,1) | D. | (-1,1) |
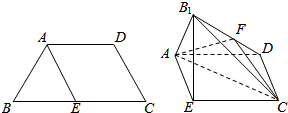 已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.
已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.