题目内容
1.已知向量$\overrightarrow{a}$=(cosα,sinα),$\overrightarrow{b}$=(cosβ,sinβ),($\overrightarrow{a}$-$\overrightarrow{b}$)2=$\frac{4}{5}$.(1)求cos(α-β)的值;
(2)-$\frac{π}{2}$<β<0<α<$\frac{π}{2}$,sinβ=-$\frac{5}{13}$,求cosα的值.
分析 (1)根据cos(α-β)=cosαcosβ+sinαsinβ进行计算;
(2)根据角的范围,求出cosβ,sin(α-β),利用cosα=sin[β+(α-β)]按照两角和正弦函数展开,代入已知以及求出的结果,即可得到cosα的值.
解答 解:(1)∵$\overrightarrow{a}$=(cosα,sinα),$\overrightarrow{b}$=(cosβ,sinβ),($\overrightarrow{a}$-$\overrightarrow{b}$)2=$\frac{4}{5}$.
∴($\overrightarrow{a}$-$\overrightarrow{b}$)2=[(cosβ-cosα)+(sinβ-sinα)]2,
=cos2β-2cosβcosα+cos2α+sin2β-2sinβ•sinα+sin2α,
=2-2(cosβcosα+sinβ•sinα)
=2-2cos(α-β)=$\frac{4}{5}$.
解得cos(α-β)=$\frac{3}{5}$;
(2)∵-$\frac{π}{2}$<β<0,sinβ=-$\frac{5}{13}$,
∴cosβ=-$\sqrt{1-si{n}^{2}β}$=-$\frac{12}{13}$.
又∵-$\frac{π}{2}$<β<0<α<$\frac{π}{2}$,
∴0<α-β<π,
∴sin(α-β)=$\sqrt{1-co{s}^{2}(α-β)}$=$\frac{4}{5}$,
∴cosα=cos[β+(α-β)]=cosβcos(α-β)-sinβsin(α-β)=(-$\frac{12}{13}$)×$\frac{3}{5}$-(-$\frac{5}{13}$)×$\frac{4}{5}$=-$\frac{56}{65}$.
即cosα=-$\frac{56}{65}$.
点评 本题考查三角函数的恒等变换及化简求值,其中角的变换cosα=sin[β+(α-β)]为解题简化过程,值得同学反思和总结.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案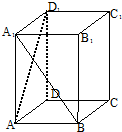 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
| A. | -3 | B. | $\frac{2}{5}$ | C. | 3 | D. | $-\frac{5}{2}$ |
| A. | $2\sqrt{2}$ | B. | $\frac{{3\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
| A. | (1,2) | B. | [1,2] | C. | [-1,1) | D. | (-1,1) |
| A. | f(2a)<f(3)<f(log2a) | B. | f(3)<f(log2a)<f(2a) | C. | f(log2a)<f(3)<f(2a) | D. | f(log2a)<f(2a)<f(3) |