题目内容
(本小题满分13分)
已知抛物线的焦点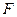 在
在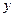 轴上,抛物线上一点
轴上,抛物线上一点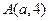 到准线的距离是
到准线的距离是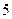 ,过点
,过点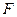 的直线与抛物线交于
的直线与抛物线交于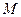 ,
,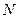 两点,过
两点,过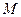 ,
,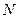 两点分别作抛物线的切线,这两条切线的交点为
两点分别作抛物线的切线,这两条切线的交点为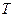 .
.
(Ⅰ)求抛物线的标准方程;
(Ⅱ)求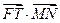 的值;
的值;
(Ⅲ)求证: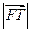 是
是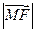 和
和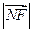 的等比中项.
的等比中项.
已知抛物线的焦点
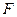 在
在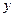 轴上,抛物线上一点
轴上,抛物线上一点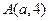 到准线的距离是
到准线的距离是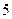 ,过点
,过点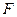 的直线与抛物线交于
的直线与抛物线交于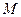 ,
,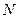 两点,过
两点,过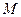 ,
,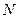 两点分别作抛物线的切线,这两条切线的交点为
两点分别作抛物线的切线,这两条切线的交点为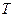 .
.(Ⅰ)求抛物线的标准方程;
(Ⅱ)求
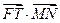 的值;
的值;(Ⅲ)求证:
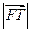 是
是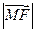 和
和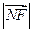 的等比中项.
的等比中项.(1)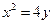 (2)0(3)略
(2)0(3)略
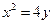 (2)0(3)略
(2)0(3)略(Ⅰ)解:由题意可设抛物线的方程为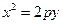
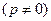 .
.
因为点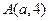 在抛物线上,所以
在抛物线上,所以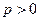 .
.
又点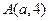 到抛物线准线的距离是
到抛物线准线的距离是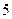 ,所以
,所以 ,可得
,可得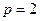 .
.
所以抛物线的标准方程为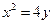 .………………………………………………3分
.………………………………………………3分
(Ⅱ)解:点 为抛物线的焦点,则
为抛物线的焦点,则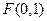 .
.
依题意可知直线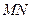 不与
不与 轴垂直,所以设直线
轴垂直,所以设直线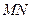 的方程为
的方程为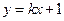 .
.
由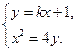 得
得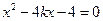 .
.
因为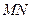 过焦点
过焦点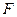 ,所以判别式大于零.
,所以判别式大于零.
设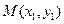 ,
,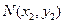 .
.
则 ,
,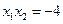 .……………………………………………………6分
.……………………………………………………6分
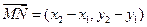
 .
.
由于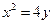 ,所以
,所以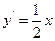 .
.
切线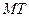 的方程为
的方程为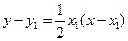 , ①
, ①
切线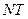 的方程为
的方程为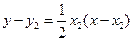 . ②
. ②
由①,②,得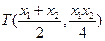 .…………………………………8分
.…………………………………8分
则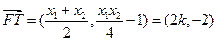 .
.
所以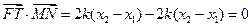 .………………………10分
.………………………10分
(Ⅲ)证明: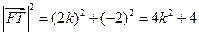 .
.
由抛物线的定义知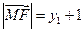 ,
,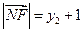 .
.
则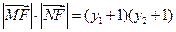
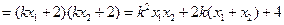
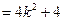 .
.
所以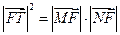 .
.
即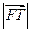 是
是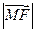 和
和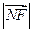 的等比中项.…………………………………………………13分
的等比中项.…………………………………………………13分
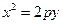
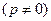 .
.因为点
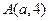 在抛物线上,所以
在抛物线上,所以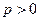 .
.又点
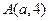 到抛物线准线的距离是
到抛物线准线的距离是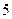 ,所以
,所以 ,可得
,可得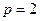 .
.所以抛物线的标准方程为
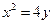 .………………………………………………3分
.………………………………………………3分(Ⅱ)解:点
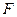 为抛物线的焦点,则
为抛物线的焦点,则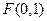 .
.依题意可知直线
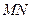 不与
不与 轴垂直,所以设直线
轴垂直,所以设直线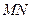 的方程为
的方程为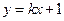 .
. 由
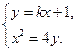 得
得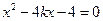 .
.因为
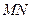 过焦点
过焦点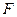 ,所以判别式大于零.
,所以判别式大于零.设
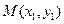 ,
,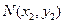 .
.则
 ,
,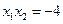 .……………………………………………………6分
.……………………………………………………6分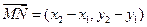
 .
.由于
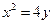 ,所以
,所以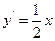 .
.切线
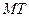 的方程为
的方程为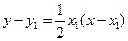 , ①
, ①切线
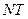 的方程为
的方程为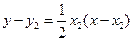 . ②
. ②由①,②,得
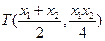 .…………………………………8分
.…………………………………8分则
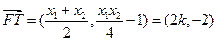 .
.所以
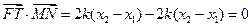 .………………………10分
.………………………10分(Ⅲ)证明:
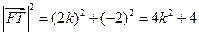 .
.由抛物线的定义知
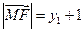 ,
,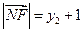 .
.则
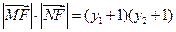
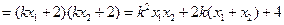
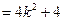 .
.所以
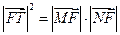 .
.即
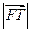 是
是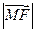 和
和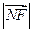 的等比中项.…………………………………………………13分
的等比中项.…………………………………………………13分
练习册系列答案
相关题目
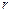 米.市场上,圆柱侧面用料单价为每平方米
米.市场上,圆柱侧面用料单价为每平方米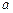 元,圆锥侧面用料单价分别是圆柱侧面用料单价和圆柱底面用料单价的4倍和2倍.设圆锥母线和底面所成角为
元,圆锥侧面用料单价分别是圆柱侧面用料单价和圆柱底面用料单价的4倍和2倍.设圆锥母线和底面所成角为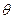 (弧度),总费用为
(弧度),总费用为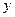 (元).
(元).
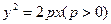 交于
交于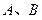 两点,且
两点,且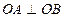 (
(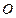 为坐标原点),
为坐标原点),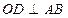 于点
于点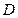 ,点
,点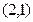
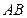 的方程
的方程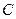 的对称中心为原点O,焦点在
的对称中心为原点O,焦点在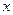 轴上,离心率为
轴上,离心率为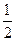 ,且点(1,
,且点(1,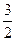 )在该椭圆上.
)在该椭圆上. 的直线
的直线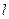 与椭圆
与椭圆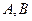 两点,若
两点,若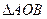 的面积为
的面积为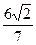 ,求圆心在原点O且与直线
,求圆心在原点O且与直线 程.
程.  的公共左右顶点,P、Q分别位于椭圆和双曲线上且不同于A、B的两点,设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4且k1+k2+k3+k4=0。
的公共左右顶点,P、Q分别位于椭圆和双曲线上且不同于A、B的两点,设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4且k1+k2+k3+k4=0。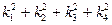 的值。
的值。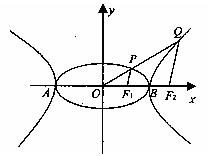
 的焦点为
的焦点为 ,过F2垂直于x轴的直线交椭圆于一点P,那么|PF1|的值是 .
,过F2垂直于x轴的直线交椭圆于一点P,那么|PF1|的值是 .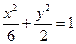 的焦点,P是曲线
的焦点,P是曲线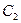 :
: 与C1的一个交点,
与C1的一个交点,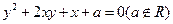 to the y-axis is
to the y-axis is  then the velue of a is
then the velue of a is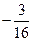
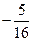
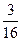
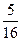
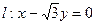 与曲线
与曲线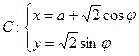
 为参数,
为参数,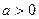 )有两个公共点A,B,且|AB|=2,则实数a的值为 ;在此条件下,以直角坐标系的原点为极点,x轴正方向为极轴建立坐标系,则曲线C的极坐标方程为 .
)有两个公共点A,B,且|AB|=2,则实数a的值为 ;在此条件下,以直角坐标系的原点为极点,x轴正方向为极轴建立坐标系,则曲线C的极坐标方程为 .