题目内容
要制作一个由同底圆锥和圆柱组成的储油罐(如图),设计要求:圆锥和圆柱的总高度和圆柱底面半径相等,都为
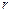 米.市场上,圆柱侧面用料单价为每平方米
米.市场上,圆柱侧面用料单价为每平方米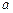 元,圆锥侧面用料单价分别是圆柱侧面用料单价和圆柱底面用料单价的4倍和2倍.设圆锥母线和底面所成角为
元,圆锥侧面用料单价分别是圆柱侧面用料单价和圆柱底面用料单价的4倍和2倍.设圆锥母线和底面所成角为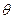 (弧度),总费用为
(弧度),总费用为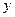 (元).
(元).(1)写出
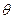 的取值范围;(2)将
的取值范围;(2)将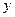 表示成
表示成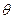 的函数关系式;
的函数关系式;(3)当
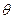 为何值时,总费用
为何值时,总费用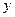 最小?
最小?
(1)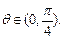 (2)同解析(3)当
(2)同解析(3)当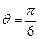 时,费用
时,费用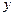 最小.
最小.
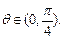 (2)同解析(3)当
(2)同解析(3)当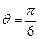 时,费用
时,费用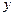 最小.
最小. 设圆锥的高为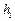 米,母线长为
米,母线长为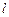 米,圆柱的高为
米,圆柱的高为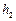 米;圆柱的侧面用料单价为每平方米2
米;圆柱的侧面用料单价为每平方米2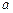 元,圆锥的侧面用料单价为每平方米4
元,圆锥的侧面用料单价为每平方米4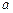 元.
元.
(1)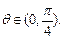
(2)圆锥的侧面用料费用为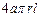 ,圆柱的侧面费用为
,圆柱的侧面费用为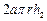 ,圆柱的地面费用为
,圆柱的地面费用为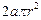 ,
,
则
 =
=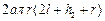 =
=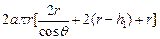 , =
, =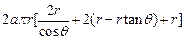 =
=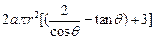 .
.
(3)设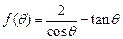 ,其中
,其中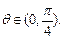 ..则
..则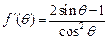 ,
,
当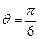 时,
时,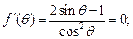
当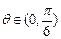 时,
时,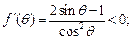 当
当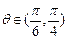 时,
时,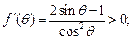
则当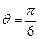 时,
时,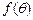 取得最小值,
取得最小值,
则当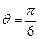 时,费用
时,费用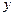 最小.
最小.
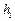 米,母线长为
米,母线长为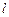 米,圆柱的高为
米,圆柱的高为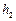 米;圆柱的侧面用料单价为每平方米2
米;圆柱的侧面用料单价为每平方米2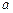 元,圆锥的侧面用料单价为每平方米4
元,圆锥的侧面用料单价为每平方米4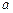 元.
元. (1)
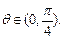
(2)圆锥的侧面用料费用为
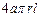 ,圆柱的侧面费用为
,圆柱的侧面费用为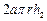 ,圆柱的地面费用为
,圆柱的地面费用为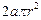 ,
, 则
 =
=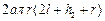 =
=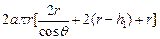 , =
, =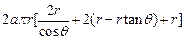 =
=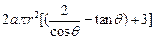 .
. (3)设
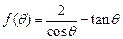 ,其中
,其中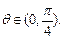 ..则
..则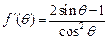 ,
, 当
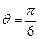 时,
时,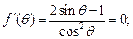
当
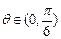 时,
时,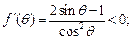 当
当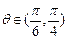 时,
时,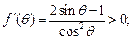
则当
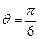 时,
时,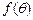 取得最小值,
取得最小值, 则当
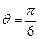 时,费用
时,费用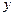 最小.
最小. 
练习册系列答案
相关题目
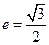 .直线
.直线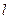 :
: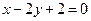 与椭圆C相交于
与椭圆C相交于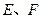 两点, 且
两点, 且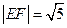
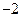 ,0),A、B为椭圆C上的动点,当
,0),A、B为椭圆C上的动点,当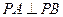 时,求证:直线AB恒过一个定点.并求出该定点的坐标.
时,求证:直线AB恒过一个定点.并求出该定点的坐标.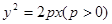 与双曲线
与双曲线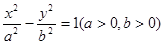 有相同的焦点
有相同的焦点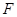 ,点
,点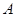 是两曲线的一个交点,
是两曲线的一个交点,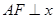 轴,若直线
轴,若直线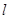 是双曲线的一条渐近线,则直线
是双曲线的一条渐近线,则直线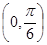

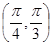
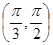
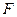 在
在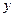 轴上,抛物线上一点
轴上,抛物线上一点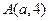 到准线的距离是
到准线的距离是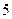 ,过点
,过点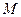 ,
,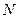 两点,过
两点,过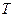 .
.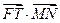 的值;
的值;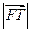 是
是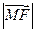 和
和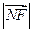 的等比中项.
的等比中项.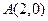 ,B、C在
,B、C在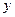 轴上,且
轴上,且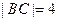 ,
,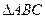 外心的轨迹
外心的轨迹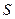 的方程;
的方程;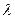 范围,使
范围,使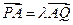 ,且
,且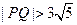 。
。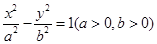 的两个顶点三等分焦距,则该双曲线的渐近线方程是
的两个顶点三等分焦距,则该双曲线的渐近线方程是



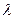
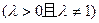 ,则动点M的轨迹是圆;
,则动点M的轨迹是圆;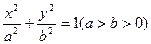 的离心率为
的离心率为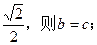
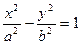
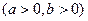 的焦点到渐近线的距离是
的焦点到渐近线的距离是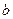 ;
;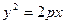 上两点
上两点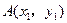 ,
, 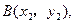 且
且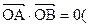
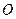 为原点),则
为原点),则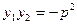 .
.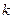 ,那么甲的面积是乙的面积的
,那么甲的面积是乙的面积的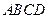 、乙:小矩形
、乙:小矩形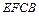 )、②(甲
)、②(甲 :大直角三角形
:大直角三角形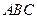 乙:小直角三角形
乙:小直角三角形 )中体会这个原理,现在图③中的曲线分别是
)中体会这个原理,现在图③中的曲线分别是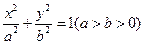 与
与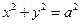 ,运用上面的原理,图③中椭圆的面积为 .
,运用上面的原理,图③中椭圆的面积为 .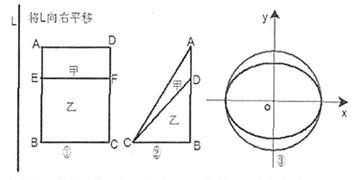
 N)=( )
N)=( ) }
}