题目内容
(本题满分12分)已知椭圆E: (其中
(其中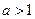 ),直 线L与椭圆只有一个公共点T;两条平行于y轴的直线
),直 线L与椭圆只有一个公共点T;两条平行于y轴的直线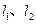 分别过椭圆的左、右焦点F1、F2,且直线L分别相交于A、B两点.
分别过椭圆的左、右焦点F1、F2,且直线L分别相交于A、B两点.
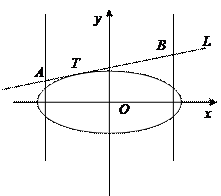
(Ⅰ)若直线L在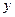 轴上的截距为
轴上的截距为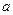 ,求证:直线L斜率的绝对值与椭圆E的离心率相等;(Ⅱ)若
,求证:直线L斜率的绝对值与椭圆E的离心率相等;(Ⅱ)若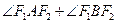 的最大值为1200,求椭圆E的方程.
的最大值为1200,求椭圆E的方程.
 (其中
(其中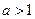 ),直 线L与椭圆只有一个公共点T;两条平行于y轴的直线
),直 线L与椭圆只有一个公共点T;两条平行于y轴的直线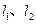 分别过椭圆的左、右焦点F1、F2,且直线L分别相交于A、B两点.
分别过椭圆的左、右焦点F1、F2,且直线L分别相交于A、B两点.
(Ⅰ)若直线L在
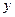 轴上的截距为
轴上的截距为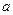 ,求证:直线L斜率的绝对值与椭圆E的离心率相等;(Ⅱ)若
,求证:直线L斜率的绝对值与椭圆E的离心率相等;(Ⅱ)若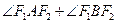 的最大值为1200,求椭圆E的方程.
的最大值为1200,求椭圆E的方程.(Ⅰ) 见解析 (Ⅱ) 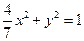
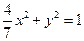
法一:(1)设T(x0,y0),由对称性,不妨设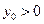 ,∴
,∴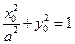 ,∴
,∴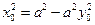 且
且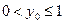 ;
;
∵直线L椭圆E只有一个公共点T,由椭圆E:
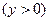 得
得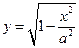 ,求导
,求导
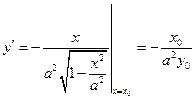 ,∴直线L:
,∴直线L: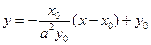 ,得
,得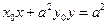 ;
;
∵直线L在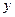 轴上的截距为
轴上的截距为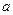 ,令
,令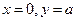 ,得
,得 ,∴
,∴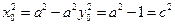 ;
;
∴直线L斜率的绝对值 ;
;
(2)直线L: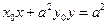 与
与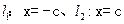 的交点
的交点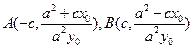 ,
,
设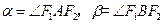 ,在RTDF1AF2和RTDF1BF2中,
,在RTDF1AF2和RTDF1BF2中,
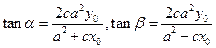 ,当
,当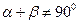 时,
时,
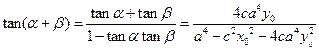
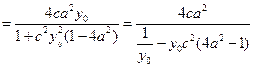 ;
;
∵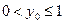 且
且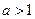 ,∴
,∴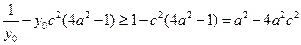 ,
,
∵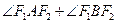 最大值为1200,只需令
最大值为1200,只需令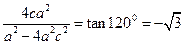 ,
,
∴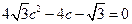 ,∴
,∴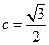 ;∴
;∴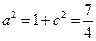 ∴椭圆E的方程为
∴椭圆E的方程为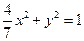 .
.
解法二:(1)依题意设直线L: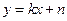 ,代入椭圆E:
,代入椭圆E: 整理得:
整理得:
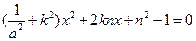 (*),∵直线L椭圆E只有一个公共点T,
(*),∵直线L椭圆E只有一个公共点T,
∴方程(*)的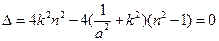 ,
,
整理得: ,①∵直线L在
,①∵直线L在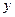 轴上的截距为
轴上的截距为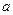 ,∴
,∴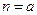 代入①得
代入①得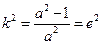 ,∴
,∴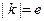 ;
;
(2)考虑对称性,不妨设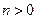 ,由①得
,由①得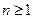 ,直线L:
,直线L: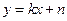 与
与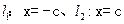 的交点
的交点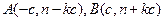 ,设
,设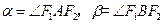 ,在RTDF1AF2和RTDF1BF2中,
,在RTDF1AF2和RTDF1BF2中,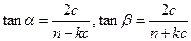 ,由①得
,由①得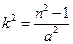 ,
,
当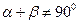 时,
时,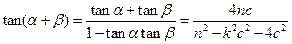
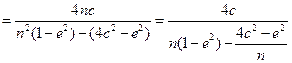 ,∵
,∵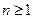 且
且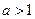 ,
,
∴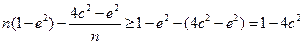 ,
,
∵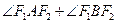 最大值为1200,只需令
最大值为1200,只需令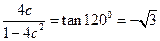 ,∴
,∴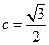 ;
;
∴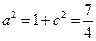 ∴椭圆E的方程为
∴椭圆E的方程为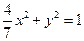 .
.
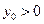 ,∴
,∴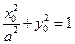 ,∴
,∴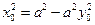 且
且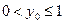 ;
;∵直线L椭圆E只有一个公共点T,由椭圆E:

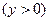 得
得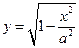 ,求导
,求导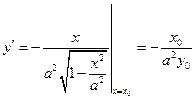 ,∴直线L:
,∴直线L: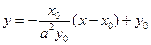 ,得
,得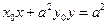 ;
;∵直线L在
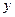 轴上的截距为
轴上的截距为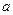 ,令
,令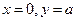 ,得
,得 ,∴
,∴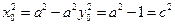 ;
;∴直线L斜率的绝对值
 ;
;(2)直线L:
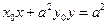 与
与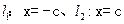 的交点
的交点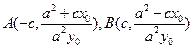 ,
,设
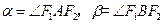 ,在RTDF1AF2和RTDF1BF2中,
,在RTDF1AF2和RTDF1BF2中,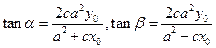 ,当
,当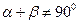 时,
时,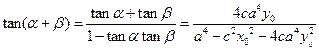
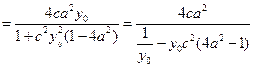 ;
;∵
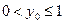 且
且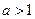 ,∴
,∴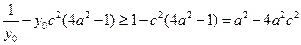 ,
,∵
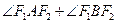 最大值为1200,只需令
最大值为1200,只需令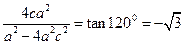 ,
,∴
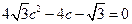 ,∴
,∴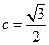 ;∴
;∴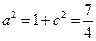 ∴椭圆E的方程为
∴椭圆E的方程为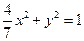 .
.解法二:(1)依题意设直线L:
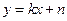 ,代入椭圆E:
,代入椭圆E: 整理得:
整理得: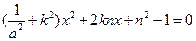 (*),∵直线L椭圆E只有一个公共点T,
(*),∵直线L椭圆E只有一个公共点T,∴方程(*)的
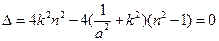 ,
,整理得:
 ,①∵直线L在
,①∵直线L在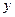 轴上的截距为
轴上的截距为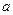 ,∴
,∴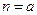 代入①得
代入①得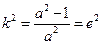 ,∴
,∴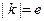 ;
;(2)考虑对称性,不妨设
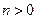 ,由①得
,由①得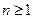 ,直线L:
,直线L: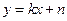 与
与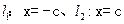 的交点
的交点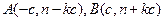 ,设
,设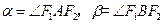 ,在RTDF1AF2和RTDF1BF2中,
,在RTDF1AF2和RTDF1BF2中,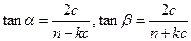 ,由①得
,由①得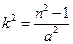 ,
,当
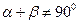 时,
时,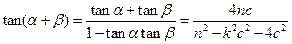
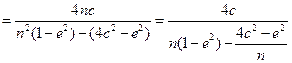 ,∵
,∵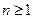 且
且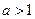 ,
,∴
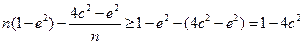 ,
,∵
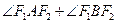 最大值为1200,只需令
最大值为1200,只需令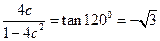 ,∴
,∴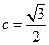 ;
;∴
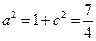 ∴椭圆E的方程为
∴椭圆E的方程为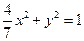 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,直线
,直线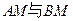 相交于点
相交于点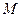 ,且它们的斜率之积为
,且它们的斜率之积为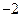 ,
,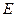 的方程;
的方程;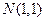 的直线
的直线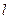 与曲线
与曲线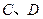 两点,且
两点,且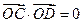 ,求直线
,求直线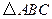 中,
中,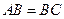 ,
,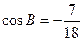 。若以
。若以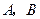 为焦点的椭圆经过点
为焦点的椭圆经过点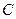 ,则该椭圆的离心率
,则该椭圆的离心率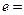 。
。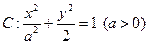 的左、右焦点分别为
的左、右焦点分别为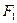 、
、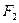 ,A是椭圆C上的一点,且
,A是椭圆C上的一点,且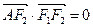 ,坐标原点O到直线
,坐标原点O到直线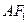 的距离为
的距离为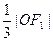 .
.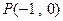 ,较y轴于点M,若
,较y轴于点M,若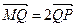 ,求直线l的方程.
,求直线l的方程.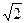 , BC="1." 以AB的中点
, BC="1." 以AB的中点 为原点建立如图8所示的平面直角坐标系
为原点建立如图8所示的平面直角坐标系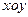 .
.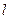 交(Ⅰ)中椭圆于M,N两点,是否存在直线
交(Ⅰ)中椭圆于M,N两点,是否存在直线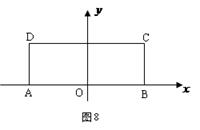
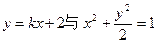 交于A、B两点,且
交于A、B两点,且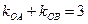 ,则直线AB的方程为: ( )
,则直线AB的方程为: ( )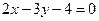 B、
B、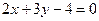
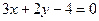 D、
D、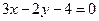
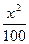 +
+ =1上的一点,F1和F2是其焦点,若∠F1PF2=60°,则△F1PF2的面积为__________________.
=1上的一点,F1和F2是其焦点,若∠F1PF2=60°,则△F1PF2的面积为__________________. +y2=1(a>1)短轴的一个端点B(0,1)为直角顶点作椭圆的内接等腰直角三角形,问这样的直角三角形是否存在?如果存在,请说明理由,并判断最多能作出几个这样的三角形;如果不存在,请说明理由.
+y2=1(a>1)短轴的一个端点B(0,1)为直角顶点作椭圆的内接等腰直角三角形,问这样的直角三角形是否存在?如果存在,请说明理由,并判断最多能作出几个这样的三角形;如果不存在,请说明理由. 的最小值是( )
的最小值是( )

