题目内容
P为椭圆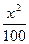 +
+ =1上的一点,F1和F2是其焦点,若∠F1PF2=60°,则△F1PF2的面积为__________________.
=1上的一点,F1和F2是其焦点,若∠F1PF2=60°,则△F1PF2的面积为__________________.
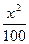 +
+ =1上的一点,F1和F2是其焦点,若∠F1PF2=60°,则△F1PF2的面积为__________________.
=1上的一点,F1和F2是其焦点,若∠F1PF2=60°,则△F1PF2的面积为__________________.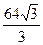
利用椭圆定义和三角形的面积公式.
∵|PF1|+|PF2|=2a=20,|F1F2|=2c=2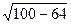 =12,
=12,
由余弦定理得|F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|cos∠F1PF2=(|PF1|+|PF2|)2-2|PF1||PF2|-2|PF1||PF2|cos∠F1PF2.
故有122=202-2|PF1||PF2|-2|PF1||PF2|cos60°.
∴3|PF1||PF2|=400-144=256.
∴|PF1||PF2|=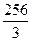 .
.
∴ =
=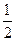 |PF1||PF2|sin60°=
|PF1||PF2|sin60°=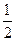 ×
×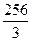 ×
×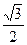 =
=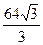 .
.
∵|PF1|+|PF2|=2a=20,|F1F2|=2c=2
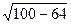 =12,
=12,由余弦定理得|F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|cos∠F1PF2=(|PF1|+|PF2|)2-2|PF1||PF2|-2|PF1||PF2|cos∠F1PF2.
故有122=202-2|PF1||PF2|-2|PF1||PF2|cos60°.
∴3|PF1||PF2|=400-144=256.
∴|PF1||PF2|=
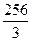 .
.∴
 =
=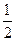 |PF1||PF2|sin60°=
|PF1||PF2|sin60°=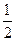 ×
×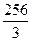 ×
×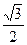 =
=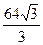 .
.
练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 (其中
(其中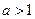 ),直 线L与椭圆只有一个公共点T;两条平行于y轴的直线
),直 线L与椭圆只有一个公共点T;两条平行于y轴的直线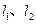 分别过椭圆的左、右焦点F1、F2,且直线L分别相交于A、B两点.
分别过椭圆的左、右焦点F1、F2,且直线L分别相交于A、B两点.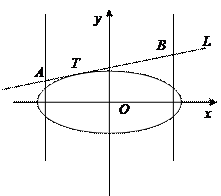
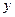 轴上的截距为
轴上的截距为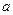 ,求证:直线L斜率的绝对值与椭圆E的离心率相等;(Ⅱ)若
,求证:直线L斜率的绝对值与椭圆E的离心率相等;(Ⅱ)若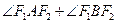 的最大值为1200,求椭圆E的方程.
的最大值为1200,求椭圆E的方程.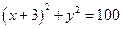 ,定点A(3,0),M为圆C上一动点,点P在AM上,点N在CM上,且满足
,定点A(3,0),M为圆C上一动点,点P在AM上,点N在CM上,且满足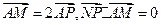 ,点N的轨迹为曲线E。
,点N的轨迹为曲线E。
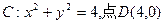 ,坐标原点为O.圆C上任意一点A在x轴上的射影为点B,已知向量
,坐标原点为O.圆C上任意一点A在x轴上的射影为点B,已知向量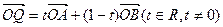 .
.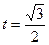 时,设动点Q关于x轴的对称点为点P,直线PD交轨迹E于点F(异于P点),证明:直线QF与x轴交于定点,并求定点坐标.
时,设动点Q关于x轴的对称点为点P,直线PD交轨迹E于点F(异于P点),证明:直线QF与x轴交于定点,并求定点坐标. 与直线
与直线 交于
交于 ,
, 两点,过原点与线段
两点,过原点与线段 中点的直线的斜率为
中点的直线的斜率为 ,则
,则 ( )
( )


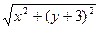 +
+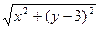 =10为不含根式的形式是( )
=10为不含根式的形式是( )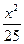 +
+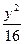 ="1"
="1"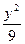 =1
=1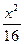 +
+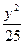 ="1"
="1"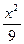 +
+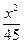 +
+ =1的两个焦点分别为F1、F2,P为椭圆上一点,且PF1⊥PF2,则||PF1|-|PF2||的值为( )
=1的两个焦点分别为F1、F2,P为椭圆上一点,且PF1⊥PF2,则||PF1|-|PF2||的值为( )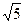
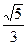

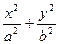 =1(a>b>0)的内接矩形面积的最大值.
=1(a>b>0)的内接矩形面积的最大值. ,且过点(2,0)的椭圆的标准方程为( )
,且过点(2,0)的椭圆的标准方程为( ) +y2=1或
+y2=1或 +
+ ="1"
="1" =1
=1