题目内容
在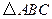 中,
中,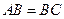 ,
,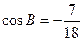 。若以
。若以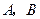 为焦点的椭圆经过点
为焦点的椭圆经过点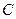 ,则该椭圆的离心率
,则该椭圆的离心率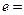 。
。
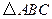 中,
中,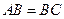 ,
,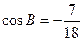 。若以
。若以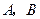 为焦点的椭圆经过点
为焦点的椭圆经过点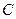 ,则该椭圆的离心率
,则该椭圆的离心率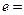 。
。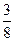
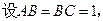 结合余弦定理求
结合余弦定理求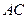 ,即
,即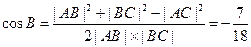 ,解得
,解得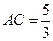 ,然后结合椭圆的定义
,然后结合椭圆的定义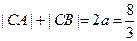 和焦距
和焦距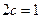 求离心率
求离心率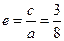 。
。
练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
题目内容
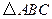 中,
中,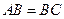 ,
,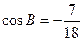 。若以
。若以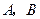 为焦点的椭圆经过点
为焦点的椭圆经过点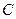 ,则该椭圆的离心率
,则该椭圆的离心率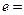 。
。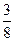
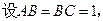 结合余弦定理求
结合余弦定理求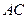 ,即
,即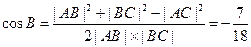 ,解得
,解得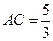 ,然后结合椭圆的定义
,然后结合椭圆的定义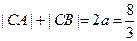 和焦距
和焦距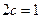 求离心率
求离心率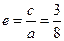 。
。
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案