题目内容
以椭圆 +y2=1(a>1)短轴的一个端点B(0,1)为直角顶点作椭圆的内接等腰直角三角形,问这样的直角三角形是否存在?如果存在,请说明理由,并判断最多能作出几个这样的三角形;如果不存在,请说明理由.
+y2=1(a>1)短轴的一个端点B(0,1)为直角顶点作椭圆的内接等腰直角三角形,问这样的直角三角形是否存在?如果存在,请说明理由,并判断最多能作出几个这样的三角形;如果不存在,请说明理由.
 +y2=1(a>1)短轴的一个端点B(0,1)为直角顶点作椭圆的内接等腰直角三角形,问这样的直角三角形是否存在?如果存在,请说明理由,并判断最多能作出几个这样的三角形;如果不存在,请说明理由.
+y2=1(a>1)短轴的一个端点B(0,1)为直角顶点作椭圆的内接等腰直角三角形,问这样的直角三角形是否存在?如果存在,请说明理由,并判断最多能作出几个这样的三角形;如果不存在,请说明理由.当1<a≤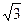 时,只能作出一个三角形;
时,只能作出一个三角形;
当a>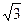 时,能作出三个三角形.
时,能作出三个三角形.
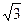 时,只能作出一个三角形;
时,只能作出一个三角形;当a>
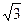 时,能作出三个三角形.
时,能作出三个三角形.由题意可知直角边BA、BC不可能垂直或平行于x轴.
故可设BC边所在直线方程为y=kx+1(不妨设k<0),则BA边所在直线方程为y=-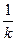 x+1.
x+1.
由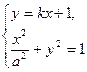 消去y,得
消去y,得
(1+a2k2)x2+2a2kx=0.
解之,得x1=0,x2=-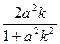 .
.
∴|BC|=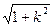 |x1-x2|=
|x1-x2|=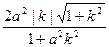 .
.
用-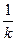 代替上式中的k得|AB|=
代替上式中的k得|AB|=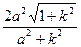 .
.
由|BC|=|BA|,得|k|(a2+k2)=1+a2k2.
注意到k<0,得(k+1)[k2+(a2-1)k+1]="0. " ①
当Δ=(a2-1)2-4<0,即1<a<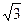 时,①有唯一解k=-1;
时,①有唯一解k=-1;
当a=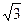 时,①化为(k+1)3=0有唯一解k=-1;
时,①化为(k+1)3=0有唯一解k=-1;
当a>3时,①有三个不同的解.
综上所述:
当1<a≤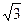 时,只能作出一个三角形;
时,只能作出一个三角形;
当a>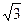 时,能作出三个三角形.
时,能作出三个三角形.
故可设BC边所在直线方程为y=kx+1(不妨设k<0),则BA边所在直线方程为y=-
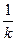 x+1.
x+1.由
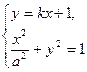 消去y,得
消去y,得(1+a2k2)x2+2a2kx=0.
解之,得x1=0,x2=-
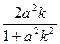 .
.∴|BC|=
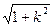 |x1-x2|=
|x1-x2|=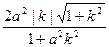 .
.用-
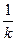 代替上式中的k得|AB|=
代替上式中的k得|AB|=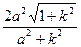 .
.由|BC|=|BA|,得|k|(a2+k2)=1+a2k2.
注意到k<0,得(k+1)[k2+(a2-1)k+1]="0. " ①
当Δ=(a2-1)2-4<0,即1<a<
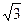 时,①有唯一解k=-1;
时,①有唯一解k=-1;当a=
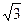 时,①化为(k+1)3=0有唯一解k=-1;
时,①化为(k+1)3=0有唯一解k=-1;当a>3时,①有三个不同的解.
综上所述:
当1<a≤
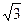 时,只能作出一个三角形;
时,只能作出一个三角形;当a>
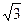 时,能作出三个三角形.
时,能作出三个三角形.
练习册系列答案
相关题目
 (其中
(其中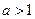 ),直 线L与椭圆只有一个公共点T;两条平行于y轴的直线
),直 线L与椭圆只有一个公共点T;两条平行于y轴的直线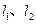 分别过椭圆的左、右焦点F1、F2,且直线L分别相交于A、B两点.
分别过椭圆的左、右焦点F1、F2,且直线L分别相交于A、B两点.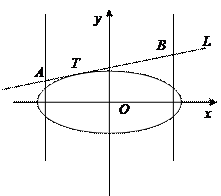
 轴上的截距为
轴上的截距为 ,求证:直线L斜率的绝对值与椭圆E的离心率相等;(Ⅱ)若
,求证:直线L斜率的绝对值与椭圆E的离心率相等;(Ⅱ)若 的最大值为1200,求椭圆E的方程.
的最大值为1200,求椭圆E的方程.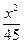 +
+ =1的两个焦点分别为F1、F2,P为椭圆上一点,且PF1⊥PF2,则||PF1|-|PF2||的值为( )
=1的两个焦点分别为F1、F2,P为椭圆上一点,且PF1⊥PF2,则||PF1|-|PF2||的值为( )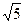
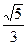

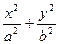 =1(a>b>0)的内接矩形面积的最大值.
=1(a>b>0)的内接矩形面积的最大值. +y2=1中斜率为1的平行弦的中点的轨迹方程是_________________.
+y2=1中斜率为1的平行弦的中点的轨迹方程是_________________. ;
; ;
; .
.

 -
-
 ,且过点(2,0)的椭圆的标准方程为( )
,且过点(2,0)的椭圆的标准方程为( ) +y2=1或
+y2=1或 +
+ ="1"
="1" =1
=1 +
+ =1与
=1与 +
+ =1(0<k<9)的关系为( )
=1(0<k<9)的关系为( )