题目内容
12.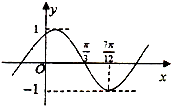 已知函数 f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到g(x)=sin 2x的图象,则只需将f (x)的图象( )
已知函数 f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到g(x)=sin 2x的图象,则只需将f (x)的图象( )| A. | 向右平移 $\frac{π}{6}$个长度单位 | B. | 向右平移 $\frac{π}{12}$个长度单位 | ||
| C. | 向左平移$\frac{π}{6}$个长度单位 | D. | 向左平移 $\frac{π}{12}$个长度单位 |
分析 由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,可得函数f(x)的解析式,再利用y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:由函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的部分图象可得A=1,
$\frac{T}{4}$=$\frac{1}{4}$•$\frac{2π}{ω}$=$\frac{7π}{12}$-$\frac{π}{3}$,求得ω=2.
再根据五点法作图可得2×$\frac{π}{3}$+φ=π,∴φ=$\frac{π}{3}$,f(x)=sin(2x+$\frac{π}{3}$).
故把f(x)=sin(2x+$\frac{π}{3}$)的图象向右平移 $\frac{π}{6}$个长度单位,可得y=sin[2(x-$\frac{π}{6}$)+$\frac{π}{3}$]=g(x)的图象,
故选:A.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
2.已知实数x,y满足ax<ay(0<a<1),则下列关系式恒成立的是( )
| A. | ln(x2+1)>ln(y2+1) | B. | sinx>siny | C. | x3>y3 | D. | $\frac{1}{{{x^2}+1}}>\frac{1}{{{y^2}+1}}$ |
3.已知奇函数f(x)的定义域为(2a,a+1),求f(a+$\frac{1}{3}$)的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
20.若等轴双曲线经过点(2,1),则该双曲线的实轴长是( )
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$ |
17.某环保部门对甲、乙两类A型品牌车各抽取5辆进行CO2排放量检测,记录如下(单位:g/km).
经测算发现,乙品牌车CO2排放量的平均值为$\overline{{x}_{乙}}$=120g/km.
(Ⅰ)从被检测的5辆甲类品牌车中任取2辆,则至少有一辆CO2排放量超过130(g/km)的概率是多少?
(Ⅱ)若90<x<130,试比较甲、乙两类品牌车CO2排放量的稳定性.
| 甲 | 80 | 110 | 120 | 140 | 150 |
| 乙 | 100 | 120 | x | y | 160 |
(Ⅰ)从被检测的5辆甲类品牌车中任取2辆,则至少有一辆CO2排放量超过130(g/km)的概率是多少?
(Ⅱ)若90<x<130,试比较甲、乙两类品牌车CO2排放量的稳定性.
4.连续抛掷两次骰子得到的点数分别为m和n,记向量$\overrightarrow{a}$=(m,n),向量$\overrightarrow{b}$=(1,-2),则$\overrightarrow{a}$⊥$\overrightarrow{b}$的概率是( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{6}$ | C. | $\frac{7}{36}$ | D. | $\frac{2}{9}$ |
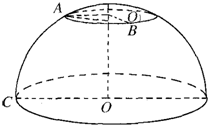 如图,在北纬60°线上,有A、B两地,它们分别在东经20°和140°线上,设地球半径为R,求A、B两地的球面距离.
如图,在北纬60°线上,有A、B两地,它们分别在东经20°和140°线上,设地球半径为R,求A、B两地的球面距离.