题目内容
2.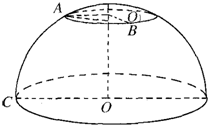 如图,在北纬60°线上,有A、B两地,它们分别在东经20°和140°线上,设地球半径为R,求A、B两地的球面距离.
如图,在北纬60°线上,有A、B两地,它们分别在东经20°和140°线上,设地球半径为R,求A、B两地的球面距离.
分析 设纬线圈半径为r,求出r,在△AO1B中,求出AB,然后求解A、B两地的球面距离$\widehat{AB}$.
解答 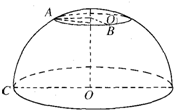 (本题满分14分)
(本题满分14分)
解:设纬线圈半径为r,据题意,∠AO1B=140°-200=1200.(2分)
∴r=Rcos∠OAO1=Rcos60°=$\frac{1}{2}R(∵∠OA{O_1}=∠AOC={60^0})$,(5分)
在△AO1B中,AB2=r2+r2-2r2•cos120°=3r3⇒AB=$\sqrt{3}r=\frac{{\sqrt{3}}}{2}$R(8分)
又在△AOB中,sin$\frac{1}{2}∠AOB=\frac{{\sqrt{3}}}{4}⇒∠AOB=2arcsin\frac{{\sqrt{3}}}{4}$(11分)
∴A、B两地的球面距离$\widehat{AB}$=2Rarcsin$\frac{\sqrt{3}}{4}$(14分)
点评 本题考查球面距离的求法,正确解题的关键是对经纬度的理解以及球面距离的解题策略.

练习册系列答案
相关题目
12.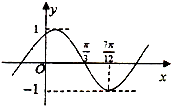 已知函数 f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到g(x)=sin 2x的图象,则只需将f (x)的图象( )
已知函数 f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到g(x)=sin 2x的图象,则只需将f (x)的图象( )
 已知函数 f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到g(x)=sin 2x的图象,则只需将f (x)的图象( )
已知函数 f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到g(x)=sin 2x的图象,则只需将f (x)的图象( )| A. | 向右平移 $\frac{π}{6}$个长度单位 | B. | 向右平移 $\frac{π}{12}$个长度单位 | ||
| C. | 向左平移$\frac{π}{6}$个长度单位 | D. | 向左平移 $\frac{π}{12}$个长度单位 |
14.随机变量X的分布列为
若p1,p2,p3成等差数列,则公差d的取值范围是[-$\frac{1}{3}$,$\frac{1}{3}$].
| X | x1 | x2 | x3 |
| P | p1 | p2 | p3 |
11.sin(-600°)=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
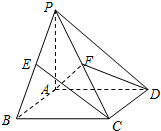 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB=2,AD=4,E、F依次是PB、PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB=2,AD=4,E、F依次是PB、PC的中点.