题目内容
2．已知实数x，y满足ax＜ay（0＜a＜1），则下列关系式恒成立的是（ ）| A． | ln（x2+1）＞ln（y2+1） | B． | sinx＞siny | C． | x3＞y3 | D． | $\frac{1}{{{x^2}+1}}＞\frac{1}{{{y^2}+1}}$ |
分析 实数x，y满足ax＜ay（0＜a＜1），可得x＞y，对于A．C．D分别举反例即可否定，对于C：由于y=x3在R上单调递增，即可判断出正误．
解答 解：∵实数x，y满足ax＜ay（0＜a＜1），
∴x＞y，
A．取x=2，b=-3，不成立；
B．取x=π，y=-π，不成立；
C．由于y=x3在R上单调递增，因此正确；
D．取x=2，y=-1，不成立．
故选：C．
点评 本题考查了函数的单调性，考查了推理能力，属于基础题．
练习册系列答案
相关题目
13．已知全集U=R，设集合A={x|y=lg（x-1）}，集合B={y|y=2x，x≥1}，则A∩（∁UB）=（ ）
| A． | [1，2] | B． | [1，2） | C． | （1，2） | D． | （1，2] |
10．对任意正数x，y，不等式$\frac{x}{3x+y}+\frac{3y}{x+3y}≤k$恒成立，则实数k的取值范围是（ ）
| A． | $[{\frac{5}{4}，+∞}）$ | B． | $[{\frac{{6-\sqrt{3}}}{4}，+∞}）$ | C． | [1，+∞） | D． | $[{\frac{{\sqrt{3}}}{2}，+∞}）$ |
7．P是双曲线$\frac{x^2}{4}$-y2=1右支（在第一象限内）上的任意一点，A1，A2分别是左右顶点，O是坐标原点，直线PA1，PO，PA2的斜率分别为k1，k2，k3，则斜率之积k1k2k3的取值范围是（ ）
| A． | （0，1） | B． | （0，$\frac{1}{8}$） | C． | （0，$\frac{1}{4}$） | D． | （0，$\frac{1}{2}$） |
14．某风景区对5个旅游景点的门票价格进行了调整，据统计，调价前后各景点的游客人数基本不变．有关数据如下表所示：
（1）该风景区称调整前后这5个景点门票的平均收费不变，平均日总收入持平．问风景区是怎样计算的？
（2）另一方面，游客认为调整收费后风景区的平均日总收入相对调整前，实际上增加了约9.4%．问游客是怎样计算的？
（3）你认为风景区和游客哪一个的说法较能反映整体情况？
| 景点 | A | B | C | D | E |
| 原价（元） | 10 | 10 | 15 | 20 | 25 |
| 现价（元） | 5 | 5 | 15 | 25 | 30 |
| 平均日人数（千人） | 1 | 1 | 2 | 3 | 2 |
（2）另一方面，游客认为调整收费后风景区的平均日总收入相对调整前，实际上增加了约9.4%．问游客是怎样计算的？
（3）你认为风景区和游客哪一个的说法较能反映整体情况？
12．
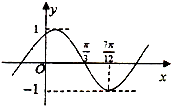已知函数 f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，为了得到g（x）=sin 2x的图象，则只需将f （x）的图象（ ）
已知函数 f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，为了得到g（x）=sin 2x的图象，则只需将f （x）的图象（ ）| A． | 向右平移 $\frac{π}{6}$个长度单位 | B． | 向右平移 $\frac{π}{12}$个长度单位 | ||
| C． | 向左平移$\frac{π}{6}$个长度单位 | D． | 向左平移 $\frac{π}{12}$个长度单位 |