Question

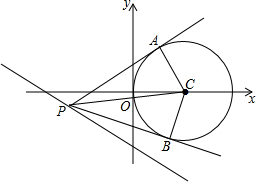
已知P是直线3x+4y+12=0上的动点，PA、PB是圆C：x²+y²-2x=0的两条切线，A、B是切点，C是圆心，求四边形PACB面积的最小值．

Answer 1

∵点P在直线3x+4y+12=0上，
∴设P（x，-3-

3

4

x），
由圆C方程变形得：（x-1）²+y²=1，即C点坐标为（1，0），
可得S_PACB=2S_PAC=|PA|•|AC|=|PA|，
∵|AP|²=|PC|²-|AC|²=|PC|²-1，
∴当|PC|最小时，|AP|最小，四边形PACB的面积最小，
∵|PC|²=（1-x）²+（3+

3

4

x）²=

25

16

（x+

4

5

）²+9，
∴|PC|²最小为9，
则S_PACB最小为2

2

．