题目内容
【题目】平行四边形![]() 中,
中,![]() ,沿
,沿![]() 将
将![]() 折起,使二面角
折起,使二面角![]() 是大小为锐角
是大小为锐角![]() 的二面角,设
的二面角,设![]() 在平面
在平面![]() 上的射影为
上的射影为![]() .
.
(1)当![]() 为何值时,三棱锥
为何值时,三棱锥![]() 的体积最大?最大值为多少?
的体积最大?最大值为多少?
(2)当![]() 时,求
时,求![]() 的大小.
的大小.
【答案】(1) 当![]() 时,三棱锥
时,三棱锥![]() 的体积最大,最大值为
的体积最大,最大值为![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题意可得BD⊥OD,可得![]() ,OC⊥平面ABDO,利用三棱锥的体积计算公式和正弦函数的单调性即可得出;
,OC⊥平面ABDO,利用三棱锥的体积计算公式和正弦函数的单调性即可得出;
(2)建立如图所示的空间直角坐标系,由![]() ,即可得出.
,即可得出.
(1)由题知OD为CD在平面ABD上的射影,![]() CO⊥平面ABD,
CO⊥平面ABD,
![]() ,∵
,∵![]() 平面
平面![]() ,
,
∴BD⊥OD,![]() 二面角
二面角![]() 的平面角
的平面角
∴![]() ,则
,则![]() .
.
∴![]()
![]()
当且仅当![]() ,即
,即![]() 时取等号,
时取等号,
∴当![]() 时,三棱锥
时,三棱锥![]() 的体积最大,最大值为
的体积最大,最大值为![]() .
.
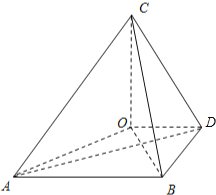
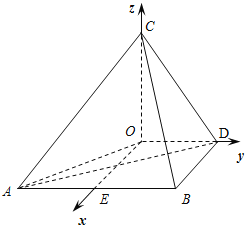
(2)过O作OE⊥AB于E,则OEBD为矩形,
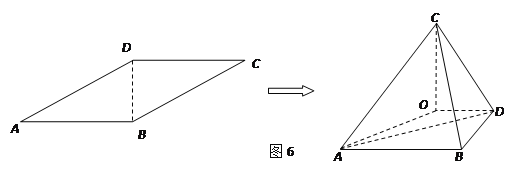
以O为原点,OE,OD,OC所在直线分别为x轴、y轴、z轴,
建立如图所示的空间直角坐标系,则
![]()
![]()
由![]() ,得
,得![]() ,
,
∴![]() ,
,
得![]() ,又
,又![]() 为锐角,∴
为锐角,∴![]() .
.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
【题目】某地有一企业2007年建厂并开始投资生产,年份代号为7,2008年年份代号为8,依次类推.经连续统计9年的收入情况如下表(经数据分析可用线性回归模型拟合![]() 与
与![]() 的关系):
的关系):
年份代号( | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
当年收入( | 13 | 14 | 18 | 20 | 21 | 22 | 24 | 28 | 29 |
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)试预测2020年该企业的收入.
(参考公式: 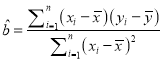
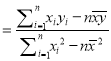 ,
, ![]() )
)