题目内容
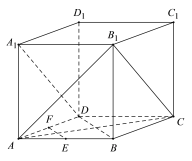
【题目】如图，在直三棱柱
中，D为A1B1的中点，AB＝BC＝2，
,
，则异面直线BD与AC所成的角为（ ）
A. 30°B. 45°C. 60°D. 90°
【答案】C
【解析】
取
的中点E，连接BE，DE，则AC∥A1C1∥DE，则∠BDE即为异面直线BD与AC所成的角,接下来根据中点的性质、中位线的性质以及勾股定理可得BD、DE和BE的关系，由此可得△BED的形状，此时即可解答本题。
如图，取B1C1的中点E，连接BE，DE，则AC∥A1C1∥DE，则∠BDE即为异面直线BD与AC所成的角.
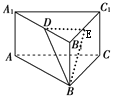
根据点D和点E分别为A1B1的中点和B1 C1的中点.利用勾股定理可得BD=BE=
。根据三角形中位线的性质可得DE=，
∴△BED为等边三角形，∴∠BDE=60°.故选C.
练习册系列答案
阅读快车系列答案
相关题目
【题目】某学校调查了20个班中有网上购物经历的人数，得到了如图所示的茎叶图，以
为分组，作出这组数的频率分布直方图，并说明频率分布直方图与茎叶图之间的关系.
0 1 2 3 | 7 3 7 6 4 4 3 0 7 5 5 4 3 2 0 8 5 4 3 0 |