题目内容
抛物线y=x2的一组斜率为2的平行弦的中点的轨迹是( )
| A.圆 | B.椭圆 | C.抛物线 | D.射线(不含端点) |
D
设平行弦中任意一条为AB,其中A(x1,y1)、B(x2,y2),AB的中点P(x,y),则由条件知
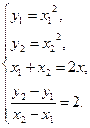
由②-①,得y2-y1=(x2-x1)(x2+x1),
即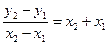 .
.
把③④代入得2=2x,即x=1.
由于弦中点必在抛物线内部,且当x=1时y=1,抛物线开口向上,所以这些平行弦的中点的轨迹方程是x=1(y>1),轨迹是去掉端点的一条射线.
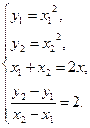
由②-①,得y2-y1=(x2-x1)(x2+x1),
即
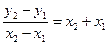 .
.把③④代入得2=2x,即x=1.
由于弦中点必在抛物线内部,且当x=1时y=1,抛物线开口向上,所以这些平行弦的中点的轨迹方程是x=1(y>1),轨迹是去掉端点的一条射线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
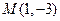 ,
,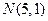 ,
,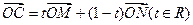 ,点C的轨迹与抛物线
,点C的轨迹与抛物线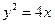 交于A、B两点.
交于A、B两点.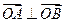 ;
;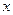 轴正半轴上是否存在一定点
轴正半轴上是否存在一定点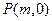 ,使得过点P的任意一条抛物线的弦的长度是原点到该弦中点距离的2倍,若存在,求出m的值;若不存在,请说明理由.
,使得过点P的任意一条抛物线的弦的长度是原点到该弦中点距离的2倍,若存在,求出m的值;若不存在,请说明理由. 上的动点
上的动点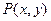 及两定点A(-2,0),B(2,0),直线PA,PB的斜率分别是
及两定点A(-2,0),B(2,0),直线PA,PB的斜率分别是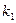 ,
,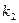 ,且
,且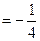 。(1)求动点P的轨迹C的方程;
。(1)求动点P的轨迹C的方程;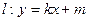 与曲线C交于M,N两点,且直线BM,BN的斜率都存在并满足
与曲线C交于M,N两点,且直线BM,BN的斜率都存在并满足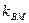 ·
·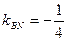 ,求证:直线
,求证:直线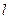 过原点。
过原点。 上的点的坐标
上的点的坐标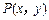 是方程
是方程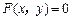 的解”是正确的,则下列命题一定正确的是( )
的解”是正确的,则下列命题一定正确的是( )
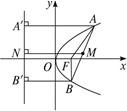
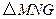 中,已知
中,已知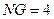 .当动点
.当动点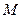 满足条件
满足条件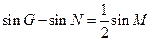 时,求动点
时,求动点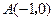 ,
, ,动点
,动点 满足
满足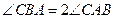 ,求动点
,求动点