题目内容
在平面直角坐标系中,O为坐标原点,已知点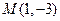 ,
,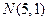 ,
,
若点C满足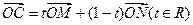 ,点C的轨迹与抛物线
,点C的轨迹与抛物线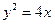 交于A、B两点.
交于A、B两点.
(I)求证: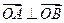 ;
;
(II)在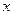 轴正半轴上是否存在一定点
轴正半轴上是否存在一定点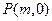 ,使得过点P的任意一条抛物线的弦的长度是原点到该弦中点距离的2倍,若存在,求出m的值;若不存在,请说明理由.
,使得过点P的任意一条抛物线的弦的长度是原点到该弦中点距离的2倍,若存在,求出m的值;若不存在,请说明理由.
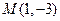 ,
,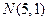 ,
,若点C满足
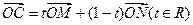 ,点C的轨迹与抛物线
,点C的轨迹与抛物线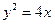 交于A、B两点.
交于A、B两点.(I)求证:
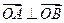 ;
;(II)在
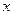 轴正半轴上是否存在一定点
轴正半轴上是否存在一定点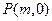 ,使得过点P的任意一条抛物线的弦的长度是原点到该弦中点距离的2倍,若存在,求出m的值;若不存在,请说明理由.
,使得过点P的任意一条抛物线的弦的长度是原点到该弦中点距离的2倍,若存在,求出m的值;若不存在,请说明理由. (I)证明见解析
(II)存在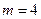 .
.
(II)存在
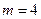 .
.(I)设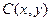 ,由
,由 知,点C的轨迹为
知,点C的轨迹为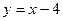 . 2分
. 2分
由 消y得:
消y得: .
.
设 ,
, ,则
,则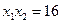 ,
,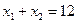 ,
,
所以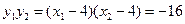 ,
,
所以 ,于是
,于是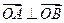 .
.
(II)假设存在过点P的弦EF符合题意,则此弦的斜率不为零,设此弦所在直线的方程为 .
.
由 消x得:
消x得: .设
.设 ,
,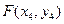 ,
,
则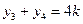 ,
,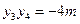 .
.
因为过点P作抛物线的弦的长度是原点到弦的中点距离的2倍,
所以 即
即 ,
,
所以 得
得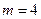 ,所以存在
,所以存在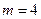 .
.
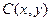 ,由
,由 知,点C的轨迹为
知,点C的轨迹为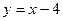 . 2分
. 2分由
 消y得:
消y得: .
.设
 ,
, ,则
,则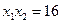 ,
,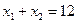 ,
, 所以
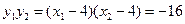 ,
,所以
 ,于是
,于是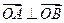 .
. (II)假设存在过点P的弦EF符合题意,则此弦的斜率不为零,设此弦所在直线的方程为
 .
.由
 消x得:
消x得: .设
.设 ,
,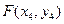 ,
,则
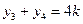 ,
,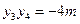 .
. 因为过点P作抛物线的弦的长度是原点到弦的中点距离的2倍,
所以
 即
即 ,
, 所以
 得
得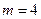 ,所以存在
,所以存在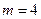 .
. 
练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
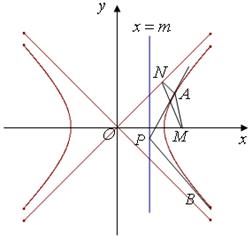
 在直线
在直线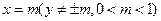 上,过点
上,过点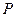 作双曲线
作双曲线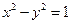 的两条切线
的两条切线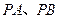 ,切点为
,切点为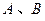 ,定点
,定点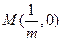 。
。
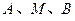 共线;
共线;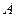 作直线
作直线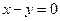 的垂线,垂足为
的垂线,垂足为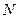 ,试求
,试求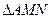 的重心
的重心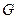 所在曲线方程。
所在曲线方程。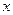 轴上,离心率为
轴上,离心率为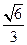 ,两条准线间的距离为6. 椭圆W的左焦点为
,两条准线间的距离为6. 椭圆W的左焦点为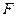 ,过左准线与
,过左准线与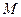 任作一条斜率不为零的直线
任作一条斜率不为零的直线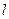 与椭圆W交于不同的两点
与椭圆W交于不同的两点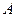 、
、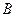 ,点
,点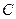 .
.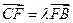 (
(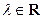 );
);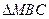 面积
面积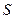 的最大值.
的最大值. 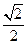 ,椭圆上的点到焦点的最短距离为1-
,椭圆上的点到焦点的最短距离为1-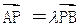 .
. 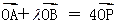 ,求m的取值范围.
,求m的取值范围.
 的直线交(1)中轨迹P、Q两点,PQ的中垂线交
的直线交(1)中轨迹P、Q两点,PQ的中垂线交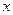 轴N. 求三角形PQN的面积.
轴N. 求三角形PQN的面积.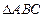 中,
中, ,AC、BC边上的高分别为BD、AE,则以A、B为焦点,且过D、E的椭圆与双曲线的离心率的倒数和为 ( )
,AC、BC边上的高分别为BD、AE,则以A、B为焦点,且过D、E的椭圆与双曲线的离心率的倒数和为 ( ) B.
B.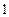 C.
C.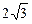 D.
D.

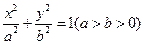 的离心率是
的离心率是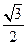 ,则双曲线
,则双曲线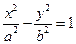 的离心率是___________
的离心率是___________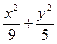 =1有一个共同的焦点,则m=______________.
=1有一个共同的焦点,则m=______________.