题目内容
在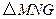 中,已知
中,已知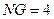 .当动点
.当动点 满足条件
满足条件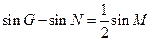 时,求动点
时,求动点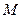 的轨迹方程.
的轨迹方程.
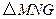 中,已知
中,已知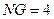 .当动点
.当动点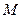 满足条件
满足条件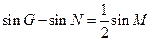 时,求动点
时,求动点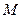 的轨迹方程.
的轨迹方程.
以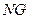 所在的直线为
所在的直线为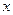 轴,以线段
轴,以线段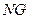 的垂直平分线为
的垂直平分线为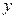 轴建立直角坐标系.
轴建立直角坐标系.
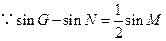 ,
,
 由正弦定理,得
由正弦定理,得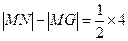 .
.
 由双曲线的定义知,点
由双曲线的定义知,点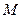 的轨迹以
的轨迹以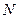 ,
,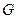 为焦点的双曲线的右支(除去与
为焦点的双曲线的右支(除去与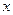 轴的交点).
轴的交点).
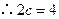 ,
,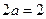 ,即
,即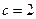 ,
,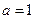 .
.
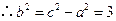 .
.
 动点
动点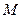 的轨迹方程为
的轨迹方程为 .
.
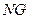 所在的直线为
所在的直线为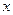 轴,以线段
轴,以线段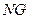 的垂直平分线为
的垂直平分线为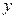 轴建立直角坐标系.
轴建立直角坐标系.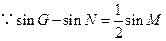 ,
, 由正弦定理,得
由正弦定理,得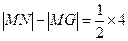 .
. 由双曲线的定义知,点
由双曲线的定义知,点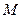 的轨迹以
的轨迹以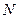 ,
,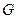 为焦点的双曲线的右支(除去与
为焦点的双曲线的右支(除去与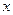 轴的交点).
轴的交点).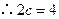 ,
,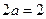 ,即
,即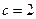 ,
,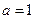 .
.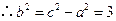 .
. 动点
动点 的轨迹方程为
的轨迹方程为 .
.
练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
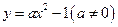 上有关于直线
上有关于直线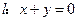 对称的不同的两点
对称的不同的两点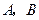 ,求实数
,求实数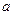 的取值范围.
的取值范围.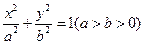 的左、右焦点分别是
的左、右焦点分别是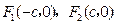 ,
,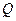 是椭圆外的动点,满足
是椭圆外的动点,满足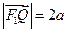 ,点
,点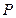 是线段
是线段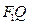 与该椭圆的交点,设
与该椭圆的交点,设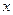 为点
为点 。
。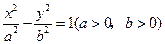 上任何一点到两条渐近线的距离之积为定值.
上任何一点到两条渐近线的距离之积为定值.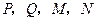 四点都在椭圆
四点都在椭圆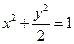 上,
上,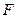 为椭圆在
为椭圆在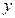 轴正半轴上的焦点.已知
轴正半轴上的焦点.已知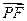 与
与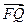 共线,
共线,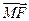 与
与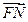 共线,且
共线,且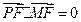 .求四边形
.求四边形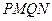 的面积的最小值和最大值.
的面积的最小值和最大值.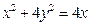 上,求使
上,求使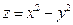 取得最大值和最小值的点
取得最大值和最小值的点 的坐标.
的坐标. 到两个定点
到两个定点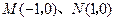 距离的比为
距离的比为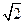 ,点
,点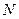 到直线
到直线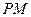 的距离为1.求直线
的距离为1.求直线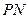 的方程.
的方程. =1有一个共同的焦点,则m=______________.
=1有一个共同的焦点,则m=______________.