��Ŀ����
4�������ij������ij��Ʒ�����м�¼�IJ���x���֣�����Ӧ�������ܺ�y���֣���ú�ļ���ͳ�����ݣ�| x | 3 | 4 | 5 | 6 | 7 |
| y | 5.8 | 8.2 | 9.7 | 12.2 | 14.1 |
��2���жϱ���x��y֮��������ػ��Ǹ���أ������Ʋ���Ϊ20��ʱ�������ܺ�Ϊ���ٶֱ�ú��
�ο���ֵ��3��5.8+4��8.2+5��9.7+6��12.2+7��14.1=270.6��
���� ��1�����������������������������С���˷�����Ҫ�ļ������ݣ�������ϵ��$\hat{b}$�Ĺ�ʽ����ý�����ٰ��������ĵ���룬���$\hat{a}$��ֵ���õ����Իع鷽�̣�
��2��������һ����������Իع鷽�̣��ɻع�ϵ������֪����ػ��Ǹ���أ���x=20�������Իع鷽�̣�Ԥ������20��ʱ�������ܺ�Ϊ���ٶֱ�ú��
��� �⣺��1����$\overline{x}$=$\frac{1}{5}$��3+4+5+6+7��=5���֣���$\overline{y}$=$\frac{1}{5}$��5.8+8.2+9.7+12.2+14.1��=10���֣���
$\sum _{i=1}^{5}$xiyi=3��5.8+4��8.2+5��9.7+6��12.2+7��14.1=270.6��
$\sum _{i=1}^{5}$xi2=9+16+25+36+49=135��
��$\hat{b}$=$\frac{270.6-5•5•10}{135-5•5•5}$=2.06��
��$\hat{a}$=10-2.06��5=-0.3��
��y����x�Ļع鷽��Ϊ$\widehat{y}$=2.06x-0.3��
��2���ɣ�1����y����x�Ļع鷽��Ϊ$\widehat{y}$=2.06x-0.3��
2.06��0����x��y֮��������أ�
��x=20ʱ��$\widehat{y}$=2.06��20-0.3=40.9��
�ʲ���Ϊ20��ʱ�������ܺ�ԼΪ40.9�ֱ�ú��
���� ���⿼�����Իع鷽�̵���������С���˷�����һ�������⣬����ʱ�������Ƚϴ�ע�����ù�ʽ��ϵ��ʱ����Ҫ�������ϳ����������е��⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | 1 | B�� | $\sqrt{2}$ | C�� | 2 | D�� | 4 |
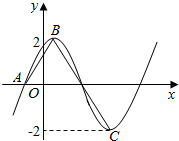 ��֪����$f��x��=2sin����x+�գ����أ�0��|��|��\frac{��}{2}��$�IJ���ͼ����ͼ��ʾ��A��B��C�ֱ��Ǻ���ͼ����x�ύ�㡢ͼ�����ߵ㡢ͼ�����͵㣮��f��0��=$\sqrt{3}$��
��֪����$f��x��=2sin����x+�գ����أ�0��|��|��\frac{��}{2}��$�IJ���ͼ����ͼ��ʾ��A��B��C�ֱ��Ǻ���ͼ����x�ύ�㡢ͼ�����ߵ㡢ͼ�����͵㣮��f��0��=$\sqrt{3}$����$\overrightarrow{AB}$•$\overrightarrow{BC}$=$\frac{{��}^{2}}{8}$-8����f��x���Ľ���ʽΪ��������
| A�� | f��x��=2sin��2x+$\frac{��}{3}$�� | B�� | f��x��=2sin��2x+$\frac{��}{6}$�� | C�� | f��x��=2sin��3x+$\frac{��}{3}$�� | D�� | f��x��=2sin��3x+$\frac{��}{6}$�� |
| A�� | $\frac{\sqrt{3}}{3}$ | B�� | 1 | C�� | $\sqrt{3}$ | D�� | $\frac{\sqrt{2}}{2}$ |
| A�� | 12 | B�� | 32 | C�� | -32 | D�� | 48 |
| A�� | ��������� | |
| B�� | ϵͳ���� | |
| C�� | �ֲ���� | |
| D�� | �ȴ��������������1�ˣ����÷ֲ���� |