题目内容
5．某小区有老年人28个，中年人57个，年轻人63个，为了调查他们的身体健康状况，从他们中抽取容量为21的样本，最适合抽取样本的方法是（ ）| A． | 简单随机抽样 | |
| B． | 系统抽样 | |
| C． | 分层抽样 | |
| D． | 先从中年人中随机剔除1人，再用分层抽样 |
分析 根据总体是由差异比较明显的几部分组成，应用分层抽样方法，
再根据总体与样本容量的比例关系，得出应从中随机剔除的个体数．
解答 解：∵（28+57+63）÷21=7余数是1，
∴应从中随机剔除1个个体；
又∵$\frac{28}{7}$=4，$\frac{63}{7}$=9，57÷7=8余数是1，
∴应先从中年人中随机剔除1人，再用分层抽样．
故选：D．
点评 本题考查了分层抽样方法的应用问题，是基础题目．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
相关题目
4．如表是某厂生产某产品过程中记录的产量x（吨）与相应的生产能耗y（吨）标准煤的几组统计数据：
（1）请根据如表提供的数据，用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$；
（2）判断变量x与y之间是正相关还是负相关，并估计产量为20吨时，生产能耗为多少吨标准煤？
参考数值：3×5.8+4×8.2+5×9.7+6×12.2+7×14.1=270.6．
| x | 3 | 4 | 5 | 6 | 7 |
| y | 5.8 | 8.2 | 9.7 | 12.2 | 14.1 |
（2）判断变量x与y之间是正相关还是负相关，并估计产量为20吨时，生产能耗为多少吨标准煤？
参考数值：3×5.8+4×8.2+5×9.7+6×12.2+7×14.1=270.6．
16．tan10°tan20°+$\sqrt{3}$（tan10°+tan20°）=（ ）
| A． | -1 | B． | $\sqrt{3}$ | C． | 1 | D． | -$\sqrt{3}$ |
20．（1-i）2•i等于（ ）
| A． | 2-2i | B． | 2+2i | C． | 2 | D． | -2 |
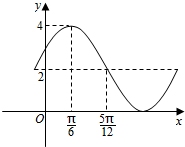已知函数y=Asin（ωx+φ）+B的一部分图象如图所示，如果A＞0，ω＞0，|φ|＜$\frac{π}{2}$，则其解析式为y=2sin（2x+$\frac{π}{6}$）+2．．
17．设集合A={1，3，4}，B={1，2，3，5}，则A∪B中元素的个数为（ ）
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |