题目内容
12.已知函数f(x)=x3-2tx2-x+1(t∈R)且f′(1)=0.(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数f(x)的极值.
分析 (1)先求导,根据f′(1)=0,求出t的值,继而求出f(x)的解析式;
(2)根据导数和函数的极值的关系即可求出.
解答 解:(Ⅰ) y=f'(x)=3x2-4tx-1,
∵f′(1)=3-4t-1=0,
∴$t=\frac{1}{2}$
即f(x)=x3-x2-x+1;
(Ⅱ)令f'(x)=3x2-2x-1=(3x+1)(x-1)=0,
解得${x_1}=-\frac{1}{3}$,x2=1,
∴
| x | (-∞,-$\frac{1}{3}$) | $-\frac{1}{3}$ | (-$\frac{1}{3}$,0) | 1 | (1,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 极大值$\frac{32}{27}$ | 极小值0 |
当x=1时有极小值f(1)=0.
点评 本题主要考查函数、导数等基本知识.考查运算求解能力及化归思想、函数方程思想、数形结合思想,属于基础题.

练习册系列答案
相关题目
2.已知直线x-2y+n=0与圆O:x2+y2=4交于A,B两点,若∠AOB=60°,则实数n的值为( )
| A. | $\sqrt{15}$ | B. | $2\sqrt{15}$ | C. | $±\sqrt{15}$ | D. | $±2\sqrt{15}$ |
3.若定义在R上的函数f(x)满足f(x+2)=f(x),且当x∈(-1,1]时,f(x)=x,则函数$y=f(x)-{log_{\frac{1}{3}}}$|x|的零点个数是( )
| A. | 0 | B. | 2 | C. | 4 | D. | 8 |
17.已知cosx=$\frac{1}{3}$,则cos2x=( )
| A. | $\frac{2}{3}$ | B. | -$\frac{8}{9}$ | C. | -$\frac{7}{9}$ | D. | $\frac{7}{9}$ |
4.如表是某厂生产某产品过程中记录的产量x(吨)与相应的生产能耗y(吨)标准煤的几组统计数据:
(1)请根据如表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(2)判断变量x与y之间是正相关还是负相关,并估计产量为20吨时,生产能耗为多少吨标准煤?
参考数值:3×5.8+4×8.2+5×9.7+6×12.2+7×14.1=270.6.
| x | 3 | 4 | 5 | 6 | 7 |
| y | 5.8 | 8.2 | 9.7 | 12.2 | 14.1 |
(2)判断变量x与y之间是正相关还是负相关,并估计产量为20吨时,生产能耗为多少吨标准煤?
参考数值:3×5.8+4×8.2+5×9.7+6×12.2+7×14.1=270.6.
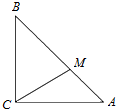 如图,在△ABC中,∠ACB=90°,且AC=BC=3,点M满足$\overrightarrow{BM}=2\overrightarrow{MA}$,
如图,在△ABC中,∠ACB=90°,且AC=BC=3,点M满足$\overrightarrow{BM}=2\overrightarrow{MA}$,