题目内容
9.已知函数f(x)满足:①对于任意实数x,y都有f(x+y)+1=f(x)+f(x),且f($\frac{1}{2}$)=0;②当x>$\frac{1}{2}$时,f(x)<0.(1)求证:f(x)=$\frac{1}{2}$+$\frac{1}{2}$f(2x);
(2)用数学归纳法证明:当x∈[$\frac{1}{{2}^{n+1}}$,$\frac{1}{{2}^{n}}$](n∈N*)时,f(x)≤1-$\frac{1}{{2}^{n}}$.
分析 (1)令y=x可得f(x)=$\frac{1}{2}$+$\frac{1}{2}$f(2x);
(2)根据数学归纳法的证明步骤,即可证明结论.
解答 证明:(1)令y=x可得f(2x)+1=f(x)+f(x),
所以f(x)=$\frac{1}{2}$+$\frac{1}{2}$f(2x)…(3分)
(2)①当n=1时,x∈[$\frac{1}{4}$,$\frac{1}{2}$],则2x∈[$\frac{1}{2}$,1],所以f(2x)≤0
又f(2x)+1=2f(x),所以f(x)=$\frac{1}{2}$+$\frac{1}{2}$f(2x)≤$\frac{1}{2}$=1-$\frac{1}{2}$
所以当n=1时命题成立.…(7分)
②假设n=k时命题成立,即当x∈[$\frac{1}{{2}^{k+1}}$,$\frac{1}{{2}^{k}}$](k∈N*)时,f(x)≤1-$\frac{1}{{2}^{k}}$
则当n=k+1时,x∈[$\frac{1}{{2}^{k+2}}$,$\frac{1}{{2}^{k+1}}$],2x∈[$\frac{1}{{2}^{k+1}}$,$\frac{1}{{2}^{k}}$],则
f(x)=$\frac{1}{2}$+$\frac{1}{2}$f(2x)≤$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{{2}^{k+1}}$=1-$\frac{1}{{2}^{k+1}}$
当n=k+1时命题成立.…(15分)
综上①②可知,当x∈[$\frac{1}{{2}^{n+1}}$,$\frac{1}{{2}^{n}}$](n∈N*)时,f(x)≤1-$\frac{1}{{2}^{n}}$.…(16分)
点评 本题主要考查数学归纳法,数学归纳法的基本形式:设P(n)是关于自然数n的命题,若1°P(n0)成立(奠基),2°假设P(k)成立(k≥n0),可以推出P(k+1)成立(归纳),则P(n)对一切大于等于n0的自然数n都成立.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{2}{3}$ | B. | -$\frac{8}{9}$ | C. | -$\frac{7}{9}$ | D. | $\frac{7}{9}$ |
| x | 3 | 4 | 5 | 6 | 7 |
| y | 5.8 | 8.2 | 9.7 | 12.2 | 14.1 |
(2)判断变量x与y之间是正相关还是负相关,并估计产量为20吨时,生产能耗为多少吨标准煤?
参考数值:3×5.8+4×8.2+5×9.7+6×12.2+7×14.1=270.6.
| A. | 8 | B. | 13 | C. | 21 | D. | 5 |
| A. | 第9项 | B. | 第8项 | C. | 第9项和第10项 | D. | 第8项和第9项 |
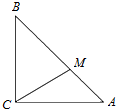 如图,在△ABC中,∠ACB=90°,且AC=BC=3,点M满足$\overrightarrow{BM}=2\overrightarrow{MA}$,
如图,在△ABC中,∠ACB=90°,且AC=BC=3,点M满足$\overrightarrow{BM}=2\overrightarrow{MA}$,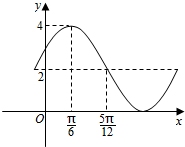 已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<$\frac{π}{2}$,则其解析式为y=2sin(2x+$\frac{π}{6}$)+2..
已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<$\frac{π}{2}$,则其解析式为y=2sin(2x+$\frac{π}{6}$)+2..