题目内容

17．如图，正方体ABCD-A1B1C1D1中，O为底面ABCD的中心，M为棱BB1的中点，则下列结论中错误的是（　　）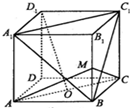
A．D1O∥平面A1BC1B．D1O⊥平面AMC
C．二面角M-AC-B等于45°D．异面直线BC1与AC所成的角等于60°

分析 根据正方体的性质以及空间线面平行、线面垂直、空间角对选项分别分析选择．

解答 解：如图，

对于A，连接B1D1，交A1C1于N，则可证明OD1∥BN，由OD1?面A1BC1，BN?面A1BC1，可得D1O∥面A1BC1，故A正确；
对于B，由三垂线定理的逆定理可得OD1⊥AC，设正方体棱长为2，可求得OM2=3，OD12=6，MD12=9，
则OD12+OM2=D1M2，有OD1⊥OM，由线面垂直的判定可得D1O⊥平面AMC，故B正确；
对于C，∠MOB为二面角M-AC-B的平面角，在Rt△MBO中，∵OB≠BM，∴二面角M-AC-B不等于45°，故C错误．
对于D，由正方体的面对角线相等得到△A1BC1为正三角形，即∠A1C1B=60°，∴异面直线BC1与AC所成的角等于60°，故D正确；
故选：C

点评 本题考查了空间直线和平面的位置关系，考查了异面直线所成角、二面角的求法，是中档题．

练习册系列答案
相关题目
7．在平面直角坐标系内，设M（x1，y1）、N（x2，y2）为不同的两点，直线l的方程为ax+by+c=0，δ=$\frac{{a{x_1}+b{y_1}+c}}{{a{x_2}+b{y_2}+c}}$．有四个判断：
①若δ=1，则过M、N两点的直线与直线l平行；
②若δ=-1，则直线l经过线段MN的中点；
③存在实数δ，使点N在直线l上；
④若δ＞1，则点M、N在直线l的同侧，且直线l与线段MN的延长线相交．
上述判断中，正确的是（　　）
A．①②③B．①②④C．①③④D．①②③④
8．若数列{an}中，a1=1，且满足an+1=2an+1，则a7=127．
5．化简$\frac{1}{{cos{{20}°}}}-\frac{{\sqrt{3}}}{{sin{{20}°}}}$=-4．
12．已知数列{an}的前n项和${S_n}=\frac{{{n^2}+n}}{2}$，数列{bn}的通项为bn=f（n），且f（n）满足：①$f（1）=\frac{1}{2}$；②对任意正整数m，n都有f（m+n）=f（m）f（n）成立．
（1）求an与bn；
（2）设数列{anbn}的前n项和为Tn，求证：$\frac{1}{2}≤{T_n}＜2$（n∈N*）；
（3）数列{bn}中是否存在三项，使得这三项按原有的顺序构成等差数列，若存在，求出这三项，若不存在，说明理由．
2．已知向量$\overrightarrow{a}$═（2，sinθ）与$\overrightarrow{b}$=（1，cosθ）互相平行，其中θ∈（0，$\frac{π}{2}$）
（1）求sin2θ和cos2θ的值；
（2）若sin（θ-φ）=$\frac{\sqrt{10}}{10}$，0＜φ＜$\frac{π}{2}$，求φ的值．
9．某学校要从5名男生和2名女生中选出3人作为志愿者，若用随机变量ξ表示选出的志愿者中女生的人数，则数学期望Eξ等于（　　）
A．$\frac{4}{7}$B．$\frac{5}{7}$C．$\frac{6}{7}$D．1
6．两个变量y与x的回归模型中，分别选择了4个不同模型，它们的相关指数R2如下，其中拟合效果最好的模型是（　　）
A．模型1的相关指数R2为0.50B．模型2的相关指数R2为0.80
C．模型3的相关指数R2为0.90D．模型4的相关指数R2为0.25
7．过原点的直线与圆x2+y2-6x+5=0相交于A，B两点，则弦AB的中点M的轨迹方程为（　　）
A．x2+y2+3x=0B．x2-y2-3x=0C．x2-y2+3x=0D．x2+y2-3x=0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网