��Ŀ����
7����ƽ��ֱ������ϵ�ڣ���M��x1��y1����N��x2��y2��Ϊ��ͬ�����㣬ֱ��l�ķ���Ϊax+by+c=0����=$\frac{{a{x_1}+b{y_1}+c}}{{a{x_2}+b{y_2}+c}}$�����ĸ��жϣ�������=1�����M��N�����ֱ����ֱ��lƽ�У�
������=-1����ֱ��l�����߶�MN���е㣻
�۴���ʵ���ģ�ʹ��N��ֱ��l�ϣ�
�����ģ�1�����M��N��ֱ��l��ͬ�࣬��ֱ��l���߶�MN���ӳ����ཻ��
�����ж��У���ȷ���ǣ�������
| A�� | �٢ڢ� | B�� | �٢ڢ� | C�� | �٢ۢ� | D�� | �٢ڢۢ� |
���� ����������ֱ�ߵ�һ��ʽ���̵��������㵽ֱ�ߵľ��빫ʽ���жϸ���ѡ���Ƿ���ȷ���Ӷ��ó����ۣ�
��� �⣺����=$\frac{{a{x_1}+b{y_1}+c}}{{a{x_2}+b{y_2}+c}}$=1����M��N���㵽ֱ��l�ľ�����ȣ���M��N������ֱ��l��ͬһ�࣬
���й�M��N�����ֱ����ֱ��lƽ�У��ʢ���ȷ��
����=$\frac{{a{x_1}+b{y_1}+c}}{{a{x_2}+b{y_2}+c}}$=-1����M��N���㵽ֱ��l�ľ�����ȣ���M��N������ֱ��l����࣬
��ֱ��l�����߶�MN���е㣬�ʢ���ȷ��
����ax2+by2+c��0���ʲ�����ʵ���ģ�ʹ��N��ֱ��l�ϣ��ʢ۲���ȷ��
���ģ�1�����M��ֱ�ߵľ�����ڵ�N��ֱ��l�ľ��룬��M��N��ֱ��l��ͬ�࣬��ֱ��l���߶�MN���ӳ����ཻ���ʢ���ȷ��
��ѡ��B��
���� ������Ҫ����ֱ�ߵ�һ��ʽ���̣��㵽ֱ�ߵľ��빫ʽ�����ڻ����⣮

��ϰ��ϵ�д�
 ��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�
�����Ŀ
5������˵������{1��2��3��4}��{4��3��2��1}��ͬһ�����ϣ���∅��{0}��ͬһ�����ϣ���{��x��y��|y=x2+1}��{y|y=x2+1}��ͬһ�����ϣ���{y|y=x+1��x��Z}��{m|m=n-1��n��Z}��ͬһ�����ϣ�������ȷ���ǣ�������
| A�� | �٢� | B�� | �٢� | C�� | �� | D�� | �٢� |
3��|a-b|=|a|+|b|�����������ǣ�������
| A�� | ab��0 | B�� | ab��1 | C�� | ab��0 | D�� | ab��1 |
17����ͼ��������ABCD-A1B1C1D1�У�OΪ����ABCD�����ģ�MΪ��BB1���е㣬�����н����д�����ǣ�������
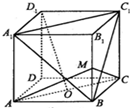

| A�� | D1O��ƽ��A1BC1 | B�� | D1O��ƽ��AMC | ||
| C�� | �����M-AC-B����45�� | D�� | ����ֱ��BC1��AC���ɵĽǵ���60�� |
 ��ͼ���ı���ABCDΪ�����Σ�PD��ƽ��ABCD��PD��QA��QA=AB=$\frac{1}{2}$PD=1��
��ͼ���ı���ABCDΪ�����Σ�PD��ƽ��ABCD��PD��QA��QA=AB=$\frac{1}{2}$PD=1��