题目内容
12.已知数列{an}的前n项和${S_n}=\frac{{{n^2}+n}}{2}$,数列{bn}的通项为bn=f(n),且f(n)满足:①$f(1)=\frac{1}{2}$;②对任意正整数m,n都有f(m+n)=f(m)f(n)成立.(1)求an与bn;
(2)设数列{anbn}的前n项和为Tn,求证:$\frac{1}{2}≤{T_n}<2$(n∈N*);
(3)数列{bn}中是否存在三项,使得这三项按原有的顺序构成等差数列,若存在,求出这三项,若不存在,说明理由.
分析 (1)根据等差数列的通项公式,结合f(m+n)=f(m)f(n)求出首项、公差,代入通项公式;
(2)代入anbn及Tn,利用错位相减法求出Tn,
(3)假设存在符合条件的三项br,bs,bt,其中正整数r,s,t满足r<s<t,根据等差中项的性质可知2bs=br+bt,2×2t-s=2×2t-r-1+1,左边为偶数,右边为奇数,判断出假设不成立.
解答 解:(1)an=$\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$=$\left\{\begin{array}{l}{1,n=1}\\{n,n≥2}\end{array}\right.$=n,
由f(m+n)=f(m)f(n) 令m=1得
f(n+1)=f(n)f(1)=$\frac{1}{2}$f(n),即bn+1=$\frac{1}{2}$bn;b1=$\frac{1}{2}$,
所以数列{bn}是以$\frac{1}{2}$为首项,$\frac{1}{2}$为公比的等比数列,所以bn=($\frac{1}{2}$)n,
(2)anbn=n•$\frac{1}{2}$n>0,所以Tn单调递增,故Tn≥T1=$\frac{1}{2}$,
又Tn=1×$\frac{1}{2}$+2×($\frac{1}{2}$)2+…+n•($\frac{1}{2}$)n,…①,
$\frac{1}{2}$Tn=1×($\frac{1}{2}$)2+2×($\frac{1}{2}$)3+…+n•($\frac{1}{2}$)n+1,…②,
①-②得$\frac{1}{2}$Tn=$\frac{1}{2}$+($\frac{1}{2}$)2+($\frac{1}{2}$)3+…+($\frac{1}{2}$)n-n•($\frac{1}{2}$)n+1=$\frac{\frac{1}{2}-(\frac{1}{2})^{n}×\frac{1}{2}}{1-\frac{1}{2}}$-n×($\frac{1}{2}$)n+1=1-($\frac{1}{2}$)n-n•($\frac{1}{2}$)n+1,
所以Tn=2-$\frac{n+2}{{2}^{n}}$<2,
综上证:$\frac{1}{2}≤{T_n}<2$(n∈N*);
(3)假设存在符合条件的三项br,bs,bt,其中正整数r,s,t满足r<s<t,
则2bs=br+bt,即2×($\frac{1}{2}$)s=($\frac{1}{2}$)r-($\frac{1}{2}$)t,两边同乘以2t得,
2×2t-s=2×2t-r-1+1,左边为偶数,右边为奇数,
故不存在.
点评 本题主要考查了数列的求和问题.考查了学生综合分析问题和解决问题的能力,属于中档题.

| A. | 4$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等边三角形 | D. | 等腰或直角三角形 |
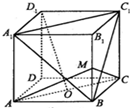
| A. | D1O∥平面A1BC1 | B. | D1O⊥平面AMC | ||
| C. | 二面角M-AC-B等于45° | D. | 异面直线BC1与AC所成的角等于60° |
| A. | sinα | B. | cosα | C. | sin$\frac{π}{3}$+cosα | D. | cos$\frac{π}{3}$+sinα |
| P(X2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
(Ⅱ)根据以上数据,能否有95%的把握认为“在恶劣气候飞行中晕机与否跟性别有关”?
附:X2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1}+{n}_{2}+n+{1}^{n}+2}$.
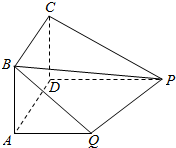 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=$\frac{1}{2}$PD=1.
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=$\frac{1}{2}$PD=1.