题目内容
6．两个变量y与x的回归模型中，分别选择了4个不同模型，它们的相关指数R2如下，其中拟合效果最好的模型是（ ）| A． | 模型1的相关指数R2为0.50 | B． | 模型2的相关指数R2为0.80 | ||
| C． | 模型3的相关指数R2为0.90 | D． | 模型4的相关指数R2为0.25 |
分析 根据两个变量y与x的回归模型中，相关指数R2越接近于1，模型的拟合效果就越好，对所给的选项选择即可．
解答 解：∵在两个变量y与x的回归模型中，它们的相关指数R2越接近于1，
这个模型的拟合效果就越好，R2越接近于0，效果就越不好；
在所给的四个选项中0.90是相关指数最大的值，
∴拟合效果最好的模型是模型3．
故选：C．
点评 本题考查了相关指数的应用问题，解题时应理解相关指数是表示模型拟合效果的量，是基础题．
练习册系列答案
小学期末冲刺100分系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
相关题目
17．如图，正方体ABCD-A1B1C1D1中，O为底面ABCD的中心，M为棱BB1的中点，则下列结论中错误的是（ ）
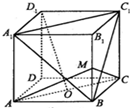
| A． | D1O∥平面A1BC1 | B． | D1O⊥平面AMC | ||
| C． | 二面角M-AC-B等于45° | D． | 异面直线BC1与AC所成的角等于60° |
14．为调查某社区居民的业余生活状况，研究这一社区居民在20：00-22：00时间段的休闲方式与性别的关系，随机调查了该社区80人，得到下面的数据表：
（Ⅰ）根据以上数据，能否有99%的把握认为“在20：00-22：00时间段居民的休闲方式与性别有关系”？
（Ⅱ）将此样本的频率估计为总体的概率，随机调查3名在该社区的男性，设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X．求X的数学期望和方差．
附：X2=$\frac{n（{n}_{11}{n}_{22}-{n}_{12}{n}_{21}）^{2}}{{n}_{1}+{n}_{2}+n+{1}^{n}+2}$．
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 10 | 50 | 60 |
| 女 | 10 | 10 | 20 |
| 合计 | 20 | 60 | 80 |
（Ⅱ）将此样本的频率估计为总体的概率，随机调查3名在该社区的男性，设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X．求X的数学期望和方差．
| P（X2≥k） | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
1．在一次恶劣气候的飞行航程中调查男女乘客在机上晕机的情况，其中男晕机人数24人，不晕机人数31人；女晕机人数8人，不晕机人数26人．
（Ⅰ）根据以上数据作2×2列联表；
（Ⅱ）根据以上数据，能否有95%的把握认为“在恶劣气候飞行中晕机与否跟性别有关”？
附：X2=$\frac{n（{n}_{11}{n}_{22}-{n}_{12}{n}_{21}）^{2}}{{n}_{1}+{n}_{2}+n+{1}^{n}+2}$．
| P（X2≥k） | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
（Ⅱ）根据以上数据，能否有95%的把握认为“在恶劣气候飞行中晕机与否跟性别有关”？
附：X2=$\frac{n（{n}_{11}{n}_{22}-{n}_{12}{n}_{21}）^{2}}{{n}_{1}+{n}_{2}+n+{1}^{n}+2}$．
