题目内容
7.过原点的直线与圆x2+y2-6x+5=0相交于A,B两点,则弦AB的中点M的轨迹方程为( )| A. | x2+y2+3x=0 | B. | x2-y2-3x=0 | C. | x2-y2+3x=0 | D. | x2+y2-3x=0 |
分析 根据圆的特殊性,设圆心为C,则有CM⊥AB,当斜率存在时,kCMkAB=-1,斜率不存在时加以验证.
解答 解:设圆x2+y2-6x+5=0的圆心为C,则C的坐标是(3,0),由题意,CM⊥AB,
①当直线CM与AB的斜率都存在时,即x≠3,x≠0时,则有kCMkAB=-1,
∴$\frac{y}{x-3}•\frac{y}{x}=-1$(x≠3,x≠0),
化简得x2+y2-3x=0(x≠3,x≠0),
②当x=3时,y=0,点(3,0)适合题意,
③当x=0时,y=0,点(0,0)不适合题意,
解方程组$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}-3x=0}\\{{x}^{2}+{y}^{2}-6x+5=0}\end{array}\right.$得x=$\frac{5}{3}$,y=$±\frac{2}{3}\sqrt{5}$,
∴点M的轨迹方程是x2+y2-3x=0($\frac{5}{3}<x≤3$).
故选:D.
点评 本题主要考查轨迹方程的求解,应注意利用圆的特殊性,同时注意所求轨迹的纯粹性,避免增解.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
17.如图,正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,M为棱BB1的中点,则下列结论中错误的是( )
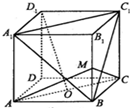

| A. | D1O∥平面A1BC1 | B. | D1O⊥平面AMC | ||
| C. | 二面角M-AC-B等于45° | D. | 异面直线BC1与AC所成的角等于60° |
12.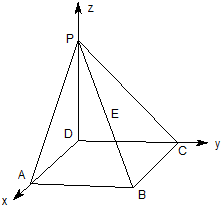 PD垂直于正方形ABCD所在平面,AB=2,E为PB的中点,cos<$\overrightarrow{DP}$,$\overrightarrow{AE}$>=$\frac{\sqrt{3}}{3}$,若以如图所示建立空间直角坐标系,则E点坐标为( )
PD垂直于正方形ABCD所在平面,AB=2,E为PB的中点,cos<$\overrightarrow{DP}$,$\overrightarrow{AE}$>=$\frac{\sqrt{3}}{3}$,若以如图所示建立空间直角坐标系,则E点坐标为( )
 PD垂直于正方形ABCD所在平面,AB=2,E为PB的中点,cos<$\overrightarrow{DP}$,$\overrightarrow{AE}$>=$\frac{\sqrt{3}}{3}$,若以如图所示建立空间直角坐标系,则E点坐标为( )
PD垂直于正方形ABCD所在平面,AB=2,E为PB的中点,cos<$\overrightarrow{DP}$,$\overrightarrow{AE}$>=$\frac{\sqrt{3}}{3}$,若以如图所示建立空间直角坐标系,则E点坐标为( )| A. | (1,1,2) | B. | (2,2,1) | C. | (1,1,1) | D. | $(1\;,\;1\;,\;\frac{1}{2})$ |
19.已知数列{an}为等比数列,a4+a14=5,a7•a11=6,则$\frac{{{a_{20}}}}{{{a_{10}}}}$=( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{3}或\frac{3}{2}$ | D. | $-\frac{2}{3}或-\frac{3}{2}$ |