题目内容
3.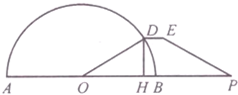 如图,AB是半径为r的半圆形广场的直径,在AB的延长线上一点P处,有一停车场,且BP=r,D为半圆上(靠近停车场一侧)的一点,在点D和P之间修建一条折线形道路DEP,已知DE∥BP,并且DE的长等于点D到AB距离DH的一半,设∠BOD=θ(O为半圆的圆心),f(θ)=$\frac{HP}{DE}$.
如图,AB是半径为r的半圆形广场的直径,在AB的延长线上一点P处,有一停车场,且BP=r,D为半圆上(靠近停车场一侧)的一点,在点D和P之间修建一条折线形道路DEP,已知DE∥BP,并且DE的长等于点D到AB距离DH的一半,设∠BOD=θ(O为半圆的圆心),f(θ)=$\frac{HP}{DE}$.(1)求函数f(θ)的解析式;
(2)求f(θ)的最小值及对应的θ值.
分析 (1)由题意可得HD=rsinθ,OH=rcosθ,从而可得HP=2r-rcosθ,DE=$\frac{1}{2}$HD=$\frac{1}{2}$rsinθ,从而化简f(θ)=$\frac{HP}{DE}$=$\frac{2r-rcosθ}{\frac{1}{2}rsinθ}$=$\frac{4-2cosθ}{sinθ}$(0<θ≤$\frac{π}{2}$);
(2)求导f′(θ)=$\frac{2sinθsinθ-(4-2cosθ)cosθ}{si{n}^{2}θ}$=$\frac{2-4cosθ}{si{n}^{2}θ}$;从而由导数判断函数的单调性再求最小值及最小值点.
解答 解:(1)由题意得,
HD=rsinθ,OH=rcosθ;
故HP=2r-rcosθ,DE=$\frac{1}{2}$HD=$\frac{1}{2}$rsinθ,
故f(θ)=$\frac{HP}{DE}$=$\frac{2r-rcosθ}{\frac{1}{2}rsinθ}$=$\frac{4-2cosθ}{sinθ}$(0<θ≤$\frac{π}{2}$);
(2)∵f(θ)=$\frac{4-2cosθ}{sinθ}$,
∴f′(θ)=$\frac{2sinθsinθ-(4-2cosθ)cosθ}{si{n}^{2}θ}$=$\frac{2-4cosθ}{si{n}^{2}θ}$;
∴当θ∈(0,$\frac{π}{3}$)时,f′(θ)<0,
当θ∈($\frac{π}{3}$,$\frac{π}{2}$]时,f′(θ)>0;
故f(θ)=$\frac{4-2cosθ}{sinθ}$在(0,$\frac{π}{3}$)上单调递减,在[$\frac{π}{3}$,$\frac{π}{2}$]上单调递增;
故当θ=$\frac{π}{3}$时,f(θ)取得最小值f($\frac{π}{3}$)=2$\sqrt{3}$.
点评 本题考查了函数在实际问题中的应用及导数的综合应用,同时考查了三角函数的应用,属于中档题.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案| A. | (-$\frac{π}{2}$,$\frac{π}{2}}$) | B. | (0,π) | C. | ($\frac{π}{2}$,$\frac{3π}{2}}$) | D. | (π,2π) |
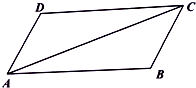 在平行四边形ABCD中,已知AB=2,AD=1,$\overrightarrow{AB}•\overrightarrow{AC}$=5,
在平行四边形ABCD中,已知AB=2,AD=1,$\overrightarrow{AB}•\overrightarrow{AC}$=5,