题目内容
13.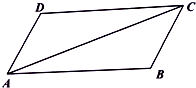 在平行四边形ABCD中,已知AB=2,AD=1,$\overrightarrow{AB}•\overrightarrow{AC}$=5,
在平行四边形ABCD中,已知AB=2,AD=1,$\overrightarrow{AB}•\overrightarrow{AC}$=5,(1)求|$\overrightarrow{AC}$|;
(2)求cos∠DAC.
分析 (1)根据向量的加法几何意义得出$\overrightarrow{AD}$$+\overrightarrow{AB}$=$\overrightarrow{AC}$,得出$\overrightarrow{AB}$$•\overrightarrow{AD}$=1,运用数量积得出cos∠DAB=$\frac{1}{2}$,即可求解角,再求解$\overrightarrow{AC}$|2=($\overrightarrow{AD}$$+\overrightarrow{AB}$)2=1+4+2×2×1×cos60°=7,即可得出|$\overrightarrow{AC}$|
(2)在△ADC中,AD=1,AC=$\sqrt{7}$,DC=2,运用余弦定理求解即可.
解答 解:(1)$\overrightarrow{AD}$$+\overrightarrow{AB}$=$\overrightarrow{AC}$,
∵AB=2,AD=1,$\overrightarrow{AB}•\overrightarrow{AC}$=5,
∴$\overrightarrow{AB}$•($\overrightarrow{AB}$$+\overrightarrow{AD}$)=5,
4+$\overrightarrow{AB}$$•\overrightarrow{AD}$=5,
∴$\overrightarrow{AB}$$•\overrightarrow{AD}$=1,
∵|$\overrightarrow{AB}$|$•|\overrightarrow{AD}|$COS∠DAB=1,
∴cos∠DAB=$\frac{1}{2}$,
∴∠DAB=60°,
∴|$\overrightarrow{AC}$|2=($\overrightarrow{AD}$$+\overrightarrow{AB}$)2=1+4+2×2×1×cos60°=7,
∴|$\overrightarrow{AC}$|=$\sqrt{7}$.
(2)在△ADC中,AD=1,AC=$\sqrt{7}$,DC=2,
根据余弦定理得出:cos∠DAC=$\frac{A{D}^{2}+A{C}^{2}-D{C}^{2}}{2AD•AC}$=$\frac{1+7-4}{2×1×\sqrt{7}}$=$\frac{2\sqrt{7}}{7}$
点评 本题综合考察了平面向量的运算,几何意义,三角形中的定理,考察了学生的计算能力,运用图形的能力.

 备战中考寒假系列答案
备战中考寒假系列答案| A. | 2 | B. | -2 | C. | ±2 | D. | $\sqrt{5}$ |
| A. | φ=$\frac{π}{3}$ | B. | φ=$\frac{π}{4}$ | C. | φ=$\frac{π}{5}$ | D. | φ=$\frac{π}{6}$ |
| A. | $\frac{\sqrt{2}}{2π}$ | B. | $\frac{1}{π}$ | C. | $\frac{\sqrt{2}}{π}$ | D. | $\frac{2}{π}$ |
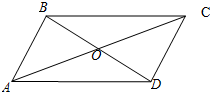 如图,在平行四边形ABCD中,BD,AC相交于点O,设向量$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$.
如图,在平行四边形ABCD中,BD,AC相交于点O,设向量$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$.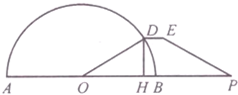 如图,AB是半径为r的半圆形广场的直径,在AB的延长线上一点P处,有一停车场,且BP=r,D为半圆上(靠近停车场一侧)的一点,在点D和P之间修建一条折线形道路DEP,已知DE∥BP,并且DE的长等于点D到AB距离DH的一半,设∠BOD=θ(O为半圆的圆心),f(θ)=$\frac{HP}{DE}$.
如图,AB是半径为r的半圆形广场的直径,在AB的延长线上一点P处,有一停车场,且BP=r,D为半圆上(靠近停车场一侧)的一点,在点D和P之间修建一条折线形道路DEP,已知DE∥BP,并且DE的长等于点D到AB距离DH的一半,设∠BOD=θ(O为半圆的圆心),f(θ)=$\frac{HP}{DE}$.