题目内容
8．若命题p：?x∈R，x=sinx，则￢p为?x∈R，x≠sinx．分析 利用特称命题的否定是全称命题，写出结果即可．
解答 解：因为特称命题的否定是全称命题，所以，命题p：?x∈R，x=sinx，则￢p为?x∈R，x≠sinx．
故答案为：?x∈R，x≠sinx
点评 本题考查命题的否定，特称命题与全称命题的否定关系，基本知识的考查．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
18．已知某简谐运动的图象经过点（0，2），且对应函数的解析式为f（x）=4sin（$\frac{π}{3}$x+φ）（|φ|＜$\frac{π}{2}$），则该简谐运动的初相φ的值为（ ）
| A． | φ=$\frac{π}{3}$ | B． | φ=$\frac{π}{4}$ | C． | φ=$\frac{π}{5}$ | D． | φ=$\frac{π}{6}$ |
16．某项测试要过两关，第一关有3种测试方案，第二关有5种测试方案，某人参加该项测试，不同的测试方法种数为（ ）
| A． | 3+5 | B． | 3×5 | C． | 35 | D． | 53 |
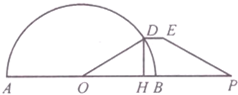如图，AB是半径为r的半圆形广场的直径，在AB的延长线上一点P处，有一停车场，且BP=r，D为半圆上（靠近停车场一侧）的一点，在点D和P之间修建一条折线形道路DEP，已知DE∥BP，并且DE的长等于点D到AB距离DH的一半，设∠BOD=θ（O为半圆的圆心），f（θ）=$\frac{HP}{DE}$．