题目内容
14.已知△ABC的三边a,b,c所对的角分别为A,B,C,且a:b:c=7:5:3.(1)求cosA的值;
(2)若△ABC的面积为45$\sqrt{3}$,求△ABC三条边长a,b,c的大小.
分析 (1)由a:b:c=7:5:3可设a=7k,b=5k,c=3k(k>0),由余弦定理得求出cosA的值;
(2)由(1)和平方关系求出sinA的值,由条件和三角形的面积公式求出三条边长a,b,c的大小.
解答 解:(1)因为a:b:c=7:5:3,
所以可设a=7k,b=5k,c=3k(k>0),…(2分)
由余弦定理得,$cosA=\frac{{{b^2}+{c^2}-{a^2}}}{2bc}$=$\frac{{{{({5k})}^2}+{{({3k})}^2}-{{({7k})}^2}}}{2×5k×3k}$=$-\frac{1}{2}$; …(4分)
(2)由(1)知,$cosA=-\frac{1}{2}$,
因为A是△ABC的内角,所以$sinA=\sqrt{1-{{cos}^2}A}$=$\frac{{\sqrt{3}}}{2}$,…(6分)
由(1)知b=5k,c=3k,因为△ABC的面积为$45\sqrt{3}$,
所以$\frac{1}{2}bcsinA=45\sqrt{3}$,…(8分)
即$\frac{1}{2}×5k×3k×\frac{{\sqrt{3}}}{2}=45\sqrt{3}$,解得$k=2\sqrt{3}$,…(10分)
解得,a=7k=$14\sqrt{3}$,b=5k=$10\sqrt{3}$,c=3k=$6\sqrt{3}$…(12分)
点评 本题考查余弦定理,平方关系的应用,以及三角形的面积公式,考查化简、计算能力,属于中档题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
4.函数f(x)=asin2x+cos2x,x∈R的最大值为$\sqrt{5}$,则实数a的值为( )
| A. | 2 | B. | -2 | C. | ±2 | D. | $\sqrt{5}$ |
2.假设四边形ABCD为圆内接正方形,向圆内随机地投一点,则点落在正方形ABCD内的概率为( )
| A. | $\frac{\sqrt{2}}{2π}$ | B. | $\frac{1}{π}$ | C. | $\frac{\sqrt{2}}{π}$ | D. | $\frac{2}{π}$ |
6.一张长方形白纸,其厚度为a,面积为b,现将此纸对折(沿对边中点连线折叠)5次,这时纸的厚度和面积分别为( )
| A. | $\frac{1}{32}$a,32b | B. | 32a,$\frac{1}{32}b$ | C. | 16a,$\frac{1}{32}b$ | D. | 16a,$\frac{1}{16}b$ |
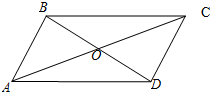 如图,在平行四边形ABCD中,BD,AC相交于点O,设向量$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$.
如图,在平行四边形ABCD中,BD,AC相交于点O,设向量$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$.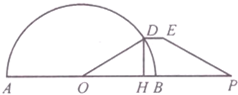 如图,AB是半径为r的半圆形广场的直径,在AB的延长线上一点P处,有一停车场,且BP=r,D为半圆上(靠近停车场一侧)的一点,在点D和P之间修建一条折线形道路DEP,已知DE∥BP,并且DE的长等于点D到AB距离DH的一半,设∠BOD=θ(O为半圆的圆心),f(θ)=$\frac{HP}{DE}$.
如图,AB是半径为r的半圆形广场的直径,在AB的延长线上一点P处,有一停车场,且BP=r,D为半圆上(靠近停车场一侧)的一点,在点D和P之间修建一条折线形道路DEP,已知DE∥BP,并且DE的长等于点D到AB距离DH的一半,设∠BOD=θ(O为半圆的圆心),f(θ)=$\frac{HP}{DE}$.