题目内容
18．某种植物的种子发芽率是0.7，则3颗种子中恰好有2颗发芽的概率是0.441．分析 由条件利用n次独立重复实验中恰好发生k次的概率计算公式，计算求的结果．
解答 解：3颗种子中恰好有2颗发芽的概率是 ${C}_{3}^{2}$×0.72×0.3=0.441，
故答案为：0.441．
点评 本题主要考查n次独立重复实验中恰好发生k次的概率计算公式，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
6．一张长方形白纸，其厚度为a，面积为b，现将此纸对折（沿对边中点连线折叠）5次，这时纸的厚度和面积分别为（ ）
| A． | $\frac{1}{32}$a，32b | B． | 32a，$\frac{1}{32}b$ | C． | 16a，$\frac{1}{32}b$ | D． | 16a，$\frac{1}{16}b$ |
13．某同学用“五点法”画函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜$\frac{π}{2}$）在某一个周期的图象时，列表并填入的部分数据如下表：
（Ⅰ）求x1，x2，x3的值及函数f（x）的表达式；
（Ⅱ）将函数f（x）的图象向左平移π个单位，可得到函数g（x）的图象，若直线y=k与函数y=f（x）g（x）的图象在[0，π]上有交点，求实数k的取值范围．
| x | $\frac{2π}{3}$ | x1 | $\frac{8π}{3}$ | x2 | x3 |
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| Asin（ωx+φ） | 0 | 2 | 0 | -2 | 0 |
（Ⅱ）将函数f（x）的图象向左平移π个单位，可得到函数g（x）的图象，若直线y=k与函数y=f（x）g（x）的图象在[0，π]上有交点，求实数k的取值范围．
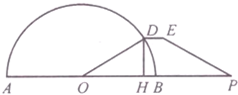如图，AB是半径为r的半圆形广场的直径，在AB的延长线上一点P处，有一停车场，且BP=r，D为半圆上（靠近停车场一侧）的一点，在点D和P之间修建一条折线形道路DEP，已知DE∥BP，并且DE的长等于点D到AB距离DH的一半，设∠BOD=θ（O为半圆的圆心），f（θ）=$\frac{HP}{DE}$．
13．已知m、n是不重合的直线，α、β是不重合的平面，则下列命题正确的是（ ）
| A． | 若m?α，n∥α，则m∥n | B． | 若m∥α，m∥β，则α∥β | ||
| C． | 若α∩β=n，m∥n，则m∥β | D． | 若m⊥α，m⊥β，则α∥β |