题目内容
12.函数y=$\frac{ln(x-1)}{\sqrt{2x-{x}^{2}}}$的定义域为(1,2).分析 根据函数成立的条件即可求函数的定义域.
解答 解:要使函数有意义,则$\left\{\begin{array}{l}{x-1>0}\\{2x-{x}^{2}>0}\end{array}\right.$,
即$\left\{\begin{array}{l}{x>1}\\{0<x<2}\end{array}\right.$,
解得1<x<2,
即函数的定义域为(1,2),
故答案为:(1,2)
点评 本题主要考查函数的定义域的求解,要求熟练掌握常见函数成立的条件.

练习册系列答案
相关题目
2.假设四边形ABCD为圆内接正方形,向圆内随机地投一点,则点落在正方形ABCD内的概率为( )
| A. | $\frac{\sqrt{2}}{2π}$ | B. | $\frac{1}{π}$ | C. | $\frac{\sqrt{2}}{π}$ | D. | $\frac{2}{π}$ |
7.某种产品的广告费支出x与销售额y(单位:百万元)之间有如表对应数据:
(1)求回归直线方程;
(2)试预测广告费支出为10百万元时,销售额多大?
$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{∑({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$.
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(2)试预测广告费支出为10百万元时,销售额多大?
$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{∑({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$.
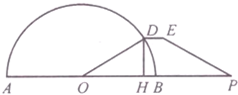 如图,AB是半径为r的半圆形广场的直径,在AB的延长线上一点P处,有一停车场,且BP=r,D为半圆上(靠近停车场一侧)的一点,在点D和P之间修建一条折线形道路DEP,已知DE∥BP,并且DE的长等于点D到AB距离DH的一半,设∠BOD=θ(O为半圆的圆心),f(θ)=$\frac{HP}{DE}$.
如图,AB是半径为r的半圆形广场的直径,在AB的延长线上一点P处,有一停车场,且BP=r,D为半圆上(靠近停车场一侧)的一点,在点D和P之间修建一条折线形道路DEP,已知DE∥BP,并且DE的长等于点D到AB距离DH的一半,设∠BOD=θ(O为半圆的圆心),f(θ)=$\frac{HP}{DE}$.