题目内容
7．新学期开始，哈六中接受6名师大学生到校实习，学校要把他们分到三个年级，每个年级2名，其中甲必须在高一年级，乙和丙均不能在高三年级，则不同的安排方法种数为（ ）| A． | 18 | B． | 15 | C． | 12 | D． | 9 |
分析 本题要先安排乙和丙两人，其安排方法可以分为两类，一类是两之一在高一，一在高二，另一类是两者都在高二，在每一类中用分步原理计算种数即可．
解答 解：若乙和丙两人有一人在高一，另一人在高二，则第一步安排高一有2种安排方法，第二步安排高二，从三人中选一人有三种方法，第二步余下两人去高三，一种方法；故此类中安排方法种数是2×3=6；
若乙和丙两人在高二，第一步安排高一，有三种安排方法，第二步安排高三，余下两人去高三，一种安排方法，故总的安排方法有3×1=3；
综上，总的安排方法种数有6+3=9种．
故选：D．
点评 本题考查分步原理与分类原理的应用，求解本题关键是根据实际情况选择正确的分类标准与分步标准，把实际问题的结构理解清楚．
练习册系列答案
相关题目
17．定义复数的一种运算z1*z2=$\frac{|{z}_{1}|+|{z}_{2}|}{2}$ （等式右边为普通运算），若复数z=a+bi，$\overline{z}$为z的共轭复数，且正实数a，b满足a+b=3，则z*$\overline{z}$的最小值为（ ）
| A． | $\frac{9}{2}$ | B． | $\frac{3\sqrt{2}}{2}$ | C． | $\frac{3}{2}$ | D． | $\frac{9}{4}$ |
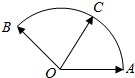给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$，它们的夹角为120°．点C在以OA，OB为半径的圆弧上，∠AOC=30°如图所示，若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$，其中x，y∈R，则x=$\frac{2\sqrt{3}}{3}$；y=$\frac{\sqrt{3}}{3}$．
15．设0＜b＜a＜1，则下列不等式不成立的是（ ）
| A． | 2b＜2a＜2 | B． | $0＜{log_{\frac{1}{2}}}a＜{log_{\frac{1}{2}}}$b | ||
| C． | ab＜b2＜1 | D． | ab＜a2＜1 |
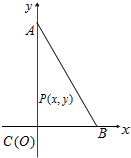设△ABC的内角A、B、C所对的边分别为a、b、c，$\frac{5（sinA-sinC）}{sin（A+C）}=\frac{5sinB-8sinC}{sinA+sinC}$，点P为△ABC内任意一点，点P到三边的距离之和为d．
12．若函数f（x）=|ax+x2-xlna-m|-3（a＞0且a≠1）有两个零点，则m的取值范围（ ）
| A． | （-2，4） | B． | （-4，2） | C． | （-1，3） | D． | （-3，1） |