题目内容
2. 设△ABC的内角A、B、C所对的边分别为a、b、c,$\frac{5(sinA-sinC)}{sin(A+C)}=\frac{5sinB-8sinC}{sinA+sinC}$,点P为△ABC内任意一点,点P到三边的距离之和为d.
设△ABC的内角A、B、C所对的边分别为a、b、c,$\frac{5(sinA-sinC)}{sin(A+C)}=\frac{5sinB-8sinC}{sinA+sinC}$,点P为△ABC内任意一点,点P到三边的距离之和为d.(1)求sinA的值;
(2)若a=3,c=5,求边b的长;
(3)在(2)的条件下,建立如图平面直角坐标系xOy,求d的取值范围.
分析 (1)根据正弦定理化简已知的式子,利用余弦定理求出cosA的值,根据内角的范围和平方关系求出sinA的值;
(2)由条件和余弦定理求出边b的值;
(3)设P(x,y),x、y>0,点P到AB边的距离是h,由等积法求出h的式子,代入d进行化简,由题意和图象列出不等式组,利用简单的线性规划问题求出h的范围,即可求出d的取值范围.
解答 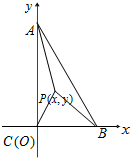 解:(1)由题意知,$\frac{5(sinA-sinC)}{sin(A+C)}=\frac{5sinB-8sinC}{sinA+sinC}$,
解:(1)由题意知,$\frac{5(sinA-sinC)}{sin(A+C)}=\frac{5sinB-8sinC}{sinA+sinC}$,
由正弦定理得,$\frac{5a-5c}{b}=\frac{5b-8c}{a+c}$,
∴5(b2+c2-a2)=8bc,
由余弦定理得,cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{4}{5}$,
∵0<A<π,∴sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{3}{5}$;
(2)把a=3、c=5代入5(b2+c2-a2)=8bc,
得5(b2+25-9)=40b,解得b=4;
(3)设P(x,y),x、y>0,连接PA、PB、PC,
设点P到AB边的距离是h,
由等积法得:S△ABC=S△PAB+S△PAC+S△PBC,
∴$\frac{1}{2}×3×4=\frac{1}{2}×4x+\frac{1}{2}×3y+\frac{1}{2}×5×h$,
则h=$\frac{-4x-3y+12}{5}$,
∴d=x+y+h=$\frac{x+2y+12}{5}$,
∵点P为△ABC内任意一点,且直线AB的方程是:4x+3y-12=0,
满足$\left\{\begin{array}{l}{x>0}\\{y>0}\\{4x+3y-12<0}\end{array}\right.$,
令z=x+2y,则y=$-\frac{1}{2}$x+$\frac{1}{2}$z,
当y=$-\frac{1}{2}$x+$\frac{1}{2}$z过点A(0,4)时,z取到最大值是8,
当y=$-\frac{1}{2}$x+$\frac{1}{2}$z过点0(0,0)时,z取到最小值是0,
∴0<x+2y<8,则$\frac{12}{5}<d<4$,
即d的取值范围是($\frac{12}{5},4$).
点评 本题考查正弦、余弦定理,平方关系和等积法的应用,以及简单的线性规划问题,注意内角的范围,属于中档题.

| A. | 1 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | -1 | D. | $\frac{{\sqrt{3}-1}}{2}$ |
| A. | 3+$\sqrt{3}$ | B. | 3-$\sqrt{3}$ | C. | 3+$\sqrt{7}$ | D. | 3-$\sqrt{7}$ |
| A. | an=$\frac{3}{2}sin({\frac{2π}{3}n-\frac{π}{6}})$ | B. | an=$\sqrt{3}sin({\frac{2π}{3}n+\frac{2π}{3}})$ | ||
| C. | an=-$\frac{3}{2}sin({\frac{2π}{3}n+\frac{5π}{6}})$ | D. | an=$\sqrt{3}sin({\frac{2π}{3}n-\frac{π}{3}})$ |
| A. | $\frac{\sqrt{6}}{4}$ | B. | $\frac{\sqrt{7}}{2}$ | C. | $\frac{\sqrt{6}}{2}$ |