题目内容
17.定义复数的一种运算z1*z2=$\frac{|{z}_{1}|+|{z}_{2}|}{2}$ (等式右边为普通运算),若复数z=a+bi,$\overline{z}$为z的共轭复数,且正实数a,b满足a+b=3,则z*$\overline{z}$的最小值为( )| A. | $\frac{9}{2}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{9}{4}$ |
分析 由新定义和复数的模长公式可得z*$\overline{z}$=$\frac{|a+bi|+|a-bi|}{2}$=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{2{a}^{2}-6a+9}$,由二次函数的最值可得.
解答 解:由题意可得z*$\overline{z}$=$\frac{|a+bi|+|a-bi|}{2}$=$\frac{\sqrt{{a}^{2}+{b}^{2}}+\sqrt{{a}^{2}+(-b)^{2}}}{2}$=$\sqrt{{a}^{2}+{b}^{2}}$,
∵正实数a,b满足a+b=3,∴b=3-a,
∴$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{{a}^{2}+(3-a)^{2}}$=$\sqrt{2{a}^{2}-6a+9}$,
由二次函数可知当a=$-\frac{-6}{2×2}$=$\frac{3}{2}$时,上式取最小值$\frac{3\sqrt{2}}{2}$
故选:B
点评 本题考查复数的运算,涉及新定义和二次函数求最值,属中档题.

练习册系列答案
相关题目
8.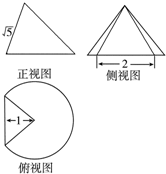 一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的表面积为( )
一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的表面积为( )
 一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的表面积为( )
一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的表面积为( )| A. | $\sqrt{5}$+$\frac{3\sqrt{3}π}{2}$+$\frac{3π}{2}$+1 | B. | 2$\sqrt{5}$+3$\sqrt{3}$π+$\frac{3π}{2}$+1 | C. | $\sqrt{5}$+$\frac{3\sqrt{3}π}{2}$+$\frac{3π}{2}$ | D. | $\sqrt{5}$+$\frac{3\sqrt{3}π}{2}$+$\frac{π}{2}$+1 |
12.已知α,β都是锐角,sinα=$\frac{1}{2}$,cosβ=$\frac{1}{2}$,则sin(α+β)=( )
| A. | 1 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | -1 | D. | $\frac{{\sqrt{3}-1}}{2}$ |
2.若$\frac{π}{2}$<α<π,化简$\sqrt{\frac{1+sinα}{1-sinα}}-\sqrt{\frac{1-sinα}{1+sinα}}$的结果是( )
| A. | -2tanα | B. | 2tanα | C. | -2cotα | D. | 2cotα |