题目内容

19．在△ABC，角A、B、C的对边分别是a、b、c，已知3cos2C-10cos（A+B）-1=0，求cosC的值．

分析 由条件利用诱导公式、二倍角的余弦公式，解方程求得cosC的值．

解答 解：△ABC中，由3cos2C-10cos（A+B）-1=0，
可得 3（2cos2C-1）+cosC-1=0，
化简可得3cos2C+5cosC-2=0，
求得cos=-2（舍去）或cosC=$\frac{1}{3}$．
综上可得，cosC=$\frac{1}{3}$．

点评 本题主要考查诱导公式、二倍角的余弦公式的应用，属于基础题．

练习册系列答案
相关题目
9．对于三次函数f（x）=ax3+bx2+cx+d（a≠0），给出定义：设f′（x）是函数y=f（x）的导数，f″（x）是f′（x）的导数，若方程f″（x）=0有实数解x0，则称点（x0，f（x0））为函数y=f（x）的“拐点”．某同学经过探究发现：任何一个三次函数都有“拐点”，任何一个三次函数都有对称中心，且“拐点”就是对称中心．
若$f（x）=\frac{1}{3}{x^3}-\frac{1}{2}{x^2}+3x-\frac{5}{12}$，请你根据这一发现，
（1）求函数$f（x）=\frac{1}{3}{x^3}-\frac{1}{2}{x^2}+3x-\frac{5}{12}$的对称中心；
（2）计算$f（{\frac{1}{2013}}）+$$f（{\frac{2}{2013}}）+$$f（{\frac{3}{2013}}）+$$f（{\frac{4}{2013}}）+$…$+f（{\frac{2012}{2013}}）$．
10．设函数f（x）=log3（9-x2）的定义域为（-3，3），值域为（-∞，2），不等式f（x）＞1的解集为（$-\sqrt{6}，\sqrt{6}$）．
7．新学期开始，哈六中接受6名师大学生到校实习，学校要把他们分到三个年级，每个年级2名，其中甲必须在高一年级，乙和丙均不能在高三年级，则不同的安排方法种数为（　　）
A．18B．15C．12D．9
14．已知函数f（x）=sin2x+$\sqrt{3}$sinxcosx-$\frac{1}{2}$．
（1）求f（x）的最小正周期．
（2）求f（x）的单调递增区间．
4．运行如图所示的程度框图，若输出结果为$\frac{4029}{2015}$，则判断框中应该填的条件是（　　）
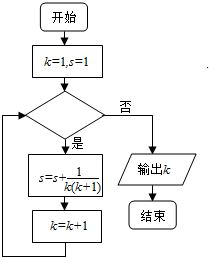
A．k＜2012B．k＜2013C．k＜2014D．k＜2015
11．设z=a+bi，a，b∈R，b≠0．，且ω=z+$\frac{1}{z}$是实数，且-1＜ω＜2．
（1）求|z|的值及z的实部的取值范围；
（2）设u=$\frac{1-z}{1+z}$，求证：u为纯虚数．
8．直线l过点P（0，1）且与直线x-y+5=0垂直，则直线l的方程是（　　）
A．x-y+1=0B．x+y-1=0C．x-y-1=0D．x+y+1=0
9．在△ABC中，BC=6，若G，O分别为△ABC的重心和外心，且$\overrightarrow{OG}$•$\overrightarrow{BC}$=6，则△ABC的形状是（　　）
A．锐角三角形B．钝角三角形
C．直角三角形D．上述三种情况都有可能

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网