题目内容
(本小题满分14分)
已知函数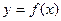 对于任意
对于任意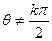 (
(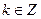 ),都有式子
),都有式子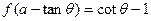 成立(其中
成立(其中 为常数).
为常数).
(Ⅰ)求函数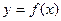 的解析式;
的解析式;
(Ⅱ)利用函数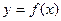 构造一个数列,方法如下:
构造一个数列,方法如下:
对于给定的定义域中的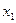 ,令
,令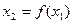 ,
,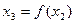 ,…,
,…,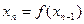 ,…
,…
在上述构造过程中,如果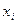 (
(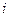 =1,2,3,…)在定义域中,那么构造数列的过程继续下去;如果
=1,2,3,…)在定义域中,那么构造数列的过程继续下去;如果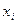 不在定义域中,那么构造数列的过程就停止.
不在定义域中,那么构造数列的过程就停止.
(ⅰ)如果可以用上述方法构造出一个常数列,求 的取值范围;
的取值范围;
(ⅱ)是否存在一个实数 ,使得取定义域中的任一值作为
,使得取定义域中的任一值作为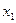 ,都可用上述方法构造出一个无穷数列
,都可用上述方法构造出一个无穷数列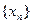 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(ⅲ)当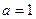 时,若
时,若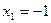 ,求数列
,求数列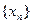 的通项公式.
的通项公式.
已知函数
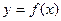 对于任意
对于任意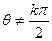 (
(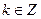 ),都有式子
),都有式子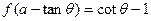 成立(其中
成立(其中 为常数).
为常数).(Ⅰ)求函数
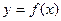 的解析式;
的解析式; (Ⅱ)利用函数
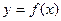 构造一个数列,方法如下:
构造一个数列,方法如下:对于给定的定义域中的
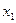 ,令
,令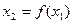 ,
,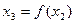 ,…,
,…,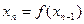 ,…
,… 在上述构造过程中,如果
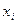 (
(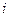 =1,2,3,…)在定义域中,那么构造数列的过程继续下去;如果
=1,2,3,…)在定义域中,那么构造数列的过程继续下去;如果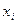 不在定义域中,那么构造数列的过程就停止.
不在定义域中,那么构造数列的过程就停止.(ⅰ)如果可以用上述方法构造出一个常数列,求
 的取值范围;
的取值范围;(ⅱ)是否存在一个实数
 ,使得取定义域中的任一值作为
,使得取定义域中的任一值作为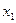 ,都可用上述方法构造出一个无穷数列
,都可用上述方法构造出一个无穷数列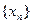 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;(ⅲ)当
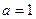 时,若
时,若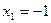 ,求数列
,求数列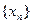 的通项公式.
的通项公式.解:(Ⅰ)令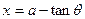 (
(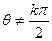 ),则
),则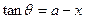 ,而
,而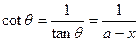 ,
,
故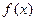 =
= ,
,
∴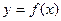 =
=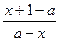 (
(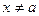 ). ………………………………3分
). ………………………………3分
(Ⅱ)(ⅰ)根据题意,只需当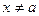 时,方程
时,方程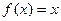 有解, ………………4分
有解, ………………4分
亦即方程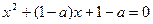 有不等于
有不等于 的解.
的解.
将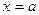 代入方程左边,左边为1,与右边不相等.故方程不可能有解
代入方程左边,左边为1,与右边不相等.故方程不可能有解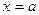 .
.
………………5分
由 △=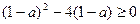 ,得
,得 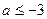 或
或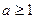 ,
,
即实数a的取值范围是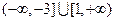 . …………………………7分
. …………………………7分
(ⅱ)假设存在一个实数 ,使得取定义域中的任一值作为x1,都可以用上述方法构造出一个无穷数列
,使得取定义域中的任一值作为x1,都可以用上述方法构造出一个无穷数列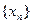 ,那么根据题意可知,
,那么根据题意可知,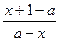 =
= 在R中无解,
在R中无解,
……………8分
亦即当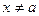 时,方程
时,方程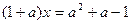 无实数解.
无实数解.
由于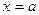 不是方程
不是方程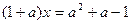 的解,
的解,
所以对于任意x∈R,方程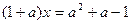 无实数解,
无实数解,
因此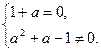 解得
解得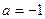 .
.
∴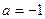 即为所求
即为所求 的值. ……………………………………11分
的值. ……………………………………11分
(ⅲ)当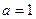 时,
时,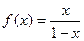 ,所以,
,所以,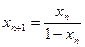 .
.
两边取倒数,得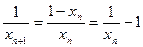 ,即
,即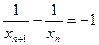 .
.
所以数列{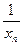 }是首项为
}是首项为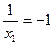 ,公差
,公差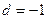 的等差数列.
的等差数列.
故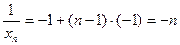 ,所以,
,所以,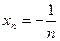 ,
,
即数列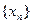 的通项公式为
的通项公式为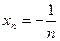 . ……………………………………14分
. ……………………………………14分
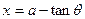 (
(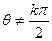 ),则
),则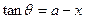 ,而
,而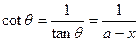 ,
,故
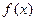 =
= ,
,∴
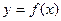 =
=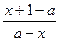 (
(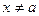 ). ………………………………3分
). ………………………………3分(Ⅱ)(ⅰ)根据题意,只需当
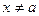 时,方程
时,方程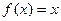 有解, ………………4分
有解, ………………4分亦即方程
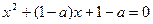 有不等于
有不等于 的解.
的解.将
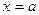 代入方程左边,左边为1,与右边不相等.故方程不可能有解
代入方程左边,左边为1,与右边不相等.故方程不可能有解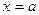 .
.………………5分
由 △=
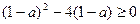 ,得
,得 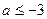 或
或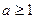 ,
,即实数a的取值范围是
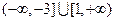 . …………………………7分
. …………………………7分(ⅱ)假设存在一个实数
 ,使得取定义域中的任一值作为x1,都可以用上述方法构造出一个无穷数列
,使得取定义域中的任一值作为x1,都可以用上述方法构造出一个无穷数列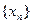 ,那么根据题意可知,
,那么根据题意可知,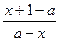 =
= 在R中无解,
在R中无解,……………8分
亦即当
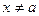 时,方程
时,方程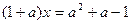 无实数解.
无实数解.由于
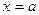 不是方程
不是方程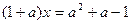 的解,
的解,所以对于任意x∈R,方程
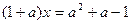 无实数解,
无实数解,因此
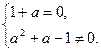 解得
解得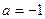 .
.∴
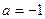 即为所求
即为所求 的值. ……………………………………11分
的值. ……………………………………11分(ⅲ)当
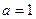 时,
时,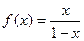 ,所以,
,所以,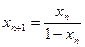 .
.两边取倒数,得
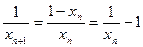 ,即
,即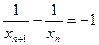 .
.所以数列{
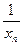 }是首项为
}是首项为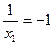 ,公差
,公差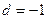 的等差数列.
的等差数列.故
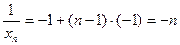 ,所以,
,所以,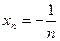 ,
,即数列
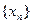 的通项公式为
的通项公式为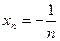 . ……………………………………14分
. ……………………………………14分
练习册系列答案
相关题目
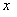 的方程
的方程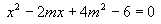 两根为
两根为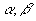 ,试求
,试求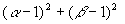 的极值。
的极值。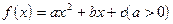 ,方程
,方程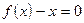 的两个根
的两个根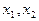 满足
满足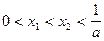 . 当
. 当 时,证明
时,证明 .
.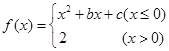 ,若
,若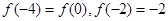 ,则关于
,则关于 的方程
的方程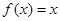 的解的个数为 ( )
的解的个数为 ( )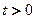 ,关于
,关于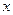 的方程
的方程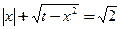 ,则这个方程有相异实根的个数情况是_________________.
,则这个方程有相异实根的个数情况是_________________.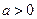 且
且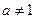 ,求使方程
,求使方程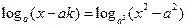 有解时的
有解时的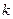 的取值范围。
的取值范围。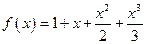 的零点的个数是 ( )
的零点的个数是 ( )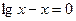 根的个数为( )
根的个数为( )